H. C. Vidya and B. R. Srivatsa Kumar
Notes on Number Theory and Discrete Mathematics
Print ISSN 1310–5132, Online ISSN 2367–8275
Volume 25, 2019, Number 4, Pages 30–43
DOI: 10.7546/nntdm.2019.25.4.30-43
Full paper (PDF, 219 Kb)
Details
Authors and affiliations
H. C. Vidya ![]()
Department of Mathematics, Manipal Institute of Technology
Manipal Academy of Higher Education, Manipal-576 104, India
B. R. Srivatsa Kumar ![]()
Department of Mathematics, Manipal Institute of Technology
Manipal Academy of Higher Education, Manipal-576 104, India
Abstract
In the present paper, we discuss some results on Eisenstein series of level 4 and 8. Also, as an application of this, we construct certain differential equations, incomplete integrals and deduce approximation to 3/π and convolution sums.
Keywords
- Theta functions
- Eisenstein series
- Convolution sums
2010 Mathematics Subject Classification
- 11M36
- 14K25
References
- Agarwal, R. P. (2010). Resonance of Ramanujan’s Mathematics (3 Volumes), New Age International Publishers.
- Alaca, A., Alaca, S. & Williams, K. S. (2006). Evaluation of the convolution
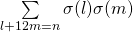 and
and 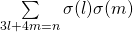 , Advances in Theoretical and Applied Mathematics, 1 (1), 27-48.
, Advances in Theoretical and Applied Mathematics, 1 (1), 27-48. - Alaca, S. & Williams, K. S. (2007). Evaluation of the convolution
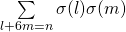 and
and 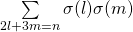 , Journal of Number Theory, 124 (2), 491–510.
, Journal of Number Theory, 124 (2), 491–510. - Alaca, A., Alaca, S. & Williams, K. S. (2007). Evaluation of the convolution
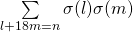 and
and 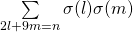 , International Mathematical Forum. Journal for Theory and Applications, 2 (1), 45–68.
, International Mathematical Forum. Journal for Theory and Applications, 2 (1), 45–68. - Alaca, A., Alaca, S. & Williams, K. S. (2007). Evaluation of the convolution
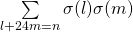 and
and 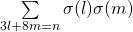 , Mathematical Journal of Okayama University, 49, 93–111.
, Mathematical Journal of Okayama University, 49, 93–111. - Alaca, A., Alaca, S. & Williams, K. S. (2008). Evaluation of the convolution
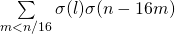 , Canadian Mathematical Bulletin, Bulletian Canadian de Mathematiques, 51 (1), 3–14.
, Canadian Mathematical Bulletin, Bulletian Canadian de Mathematiques, 51 (1), 3–14. - Andrews, G. E. & Berndt, B. C. (2009).Ramanujan’s lost Notebook,Part II, Springer, New York.
- Baruah, N. D. & Berndt, B. C. (2010). Eisenstein series and Ramanujan-Type series for 1/π, The Ramanujan Journal, 23 (1-3), 17–33.
- Berndt, B. C. (1991). Ramanujan’s Notebooks, Part III, Springer.
- Berndt, B. C. (1994). Ramanujan’s Notebooks, Part IV, Springer.
- Berndt, B. C. (1998). Ramanujan’s Notebooks, Part V, Springer.
- Berndt, B. C., Choi, G., Choi, Y.-S., Hahn, H., Yeap, B. P., Yee, A. J., Yesilyurt, H. & J.Yi. (2007). Ramanujan’s forty identities for the Rogers–Ramanujan function, Mem. Amer. Math. Soc. 188 (880), 1–96.
- Cooper, S. (2012) Sporadic sequences, modular forms and new series for 1/π, Ramanujan J., 29, 163–183.
- Cooper, S. & Ye, D. (2016). Level 14 and 15 analogous of Ramanujan’s elliptic functions to alternative bases, Transactions of the American Mathematical Society, 368 (11), 7883–7910.
- Fricke, R. (1922). Die Elliptic Funcktionen und Ihre Anwendungen, Bd. 2. B. G. Teubner, Leipzig.
- Glaisher, J. W. L. (1885). On the square of the series in which the coeff’s are the sum of the divisors of the exponents, Mess. Math., 14, 156–163.
- Glaisher, J. W. L. (1885). Mathematical Papers, Cambridge.
- Huard, J. G., Ou, Z. M., Spearman, B. K. & Williams, K. S. (2002). Elementary evaluation of certain convolution sums involving divisor functions, Number Theory for the Millennium, II, Bennett, M. A., Berndt, B. C., Boston, N., H. G. Diamond, A. J. Hildebrand and W. Philipp, Eds., 229–274.
- Lamire, M. & Williams, K. S. (2006). Evaluation of two convolution sums involving the sum of divisors function, Bulletin of the Australian Mathematical Society, 73 (1), 107–115.
- Raghavan, S. & Rangachari, S. S. (1989). On Ramanujan’s elliptic integrals and modular identities, Oxford University Press, Bombay, 119–149.
- Ramanujan, S. (1957). Notebooks (2 Volumes), Bombay.
- Ramanujan, S. (1927). Collected Papers, Cambridge University Press, Cambridge, reprinted by Chelsea, New York, 1962, reprinted by the American Mathematical Society, Providence, RI 2000.
- Ramanujan, S. (1988). The Lost Notebook and Other Unpublished Papers, Narosa.
- Royer, E. (2007). Evaluating convolution sums of the divisor function by quasimodular forms,International Journal of Number Theory, 3 (2), 231–261.
- Vasuki, K. R. & Veeresha, R. G. (2016). Ramanujan’s Eisenstein series of level 7 and 14, Journal of Number Theory, 159, 59–75.
- Williams, K. S. (2005). The convolution
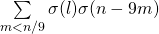 , International Journal of Number Theory, 1 (2), 193–205.
, International Journal of Number Theory, 1 (2), 193–205. - Williams, K. S. (2006). The convolution
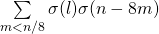 , Pacific Journal of Mathematics, 228 (2), 387–396.
, Pacific Journal of Mathematics, 228 (2), 387–396. - Xia, E. X. W. & Yao, O. X. M. (2012). Eisenstein series identities involving the Borwein’s cubic theta functions, Journal of Applied Mathematics, Article ID 181264.
Related papers
Cite this paper
Vidya, H. C. & Srivatsa Kumar, B. R. (2019). Some studies on Eisenstein series and their applications. Notes on Number Theory and Discrete Mathematics, 25(4), 30-43, DOI: 10.7546/nntdm.2019.25.4.30-43.


