On irrationality of some distances between points on a circle

Mladen Vassilev–Missana
Notes on Number Theory and Discrete Mathematics
Print ISSN 1310–5132, Online ISSN 2367–8275
Volume 22, 2016, Number 2, Pages 4–9
Full paper (PDF, 155 Kb)

Details

Authors and affiliations

Mladen Vassilev–Missana
5 Victor Hugo Str, Ap. 3
1124 Sofia, Bulgaria

Abstract

Let n > 3 be arbitrary integer. In the present paper it is shown that if K is an arbitrary circle and M_i, i = 1,…,n are points on K, dividing K into n equal arcs, then for each point M on K, different from the mentioned above, at least 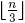of the distances |MM_i| are irrational numbers.

Keywords

• Distance
• Irrational number
• Circle

AMS Classification

• 97G40
• 11XX

References

1. Coolidge, J. L. (1939) A Historically Interesting Formula for the Area of a Quadrilateral. Amer. Math. Monthly, 46, 345–347.
2. Nagell, T. (1951) Introduction to Number Theory. Wiley, New York.
3. Mason, J. C., & Handscomb, D. C. (2003) Chebyshev Polynomials. CRC Press, New York.