Deepa Sinha and Pravin Garg
Notes on Number Theory and Discrete Mathematics, ISSN 1310–5132
Volume 19, 2013, Number 3, Pages 70–77
Full paper (PDF, 164 Kb)
Details
Authors and affiliations
Deepa Sinha ![]()
Department of Mathematics, South Asian University, Akbar Bhawan
Chanakyapuri, New Delhi–110021, India
Pravin Garg ![]()
Centre for Mathematical Sciences, Banasthali University
Banasthali–304022, Rajasthan, India
Abstract
The canonical marking on a signed graph (or sigraph, in short) S is defined as: for each vertex v ∈ V (S), μσ(v) = Πej ∈ Ev, where Ev is the set of edges ej incident at v in S. If S is canonically marked, then a cycle Z in S is said to be canonically consistent (C-consistent) if it contains an even number of negative vertices and the given sigraph S is C-consistent if every cycle in it is C-consistent. The total sigraph T(S) of a sigraph S = (V, E, σ) has T(Se) as its underlying graph and for any edge uv of T(Se),
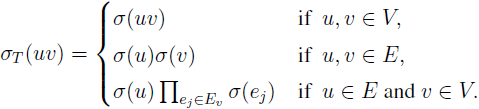
In this paper, we establish a characterization of canonically consistent total sigraphs.
Keywords
- Sigraph
- Canonical marking
- Consistent sigraph
- Total sigraph
AMS Classification
- 05C22
- 05C75
References
- Acharya, B. D. A characterization of consistent marked graphs, Nat. Acad. Sci. Lett., Vol. 6, 1983, No. 12, 431–440.
- Acharya, B. D. Some further properties of consistent marked graphs, Indian J. Pure Appl. Math., Vol. 15, 1984, No. 8, 837–842.
- Acharya, B. D. Signed intersection graphs. In preparation.
- Acharya, B. D., M. Acharya, D. Sinha. Characterization of a signed graph whose signed line graph is s-consistent, Bull. Malays. Math. Sci. Soc., Vol. 32, 2009, No. 3, 335–341.
- Akiyama, J., T. Hamada. The decompositions of line graphs, middle graphs and total graphs of complete graphs into forests, Discrete Math., Vol. 26, 1979, No. 3, 203–208.
- Behzad, M., G. Chartrand. Total graphs and traversability, Proc. Edinb. Math. Soc., Vol. 15, 1966, No. 2, 117–120.
- Behzad, M. A criterion for the planarity of the total graph of a graph, Proc. Cambridge Philos. Soc., Vol. 63, 1967, 679–681.
- Behzad, M., H. Radjavi. The total group of a graph, Proc. Amer. Math. Soc., Vol. 19, 1968, 158–163.
- Behzad, M. The connectivity of total graphs, Australian Math. Bull., Vol. 1, 1969, 175–181.
- Behzad, M., G. T. Chartrand. Line coloring of signed graphs, Elem. Math., Vol. 24, 1969, No. 3, 49–52.
- Behzad, M., H. Radjavi. Structure of regular total graphs, J. Lond. Math. Soc., Vol. 44, 1969, 433–436.
- Behzad, M. A characterization of total graphs, Proc. Amer. Math. Soc., Vol. 26, 1970, No. 3, 383–389.
- Beineke, L. W., F. Harary. Consistency in marked graphs, J. Math. Psych., Vol. 18, 1978, No. 3, 260–269.
- Beineke, L.W., F. Harary. Consistent graphs with signed points, Riv. Math. per. Sci. Econom. Sociol., Vol. 1, 1978, 81–88.
- Boza, L., M. T. D´avila, A. M´arquez, R. Moyano, Miscellaneous properties of embeddings of line, total and middle graphs, Discrete Math., Vol. 233, 2001, No. 1–3, 37–54.
- Chartrand, G. T. Graphs as Mathematical Models, Prindle, Weber and Schmidt, Inc., Boston, Massachusetts, 1977.
- Cvetkovic, D. M., S. K. Simic, Graph equations for line graphs and total graphs, Discrete Math., Vol. 13, 1975, 315–320.
- Gavril, F. A recognition algorithm for the total graphs, Networks, Vol. 8, 1978, No. 2, 121– 133.
- Harary, F. On the notion of balance of a signed graph, Mich. Math. J., Vol. 2, 1953, 143–146.
- Harary, F. Graph Theory, Addison-Wesley Publ. Comp., Reading, Massachusetts, 1969.
- Hoede, C. A characterization of consistent marked graphs, J. Graph Theory, Vol. 16, 1992, No. 1, 17–23.
- Rangarajan, R., M. S. Subramanya, P. S. K. Reddy, Neighborhood signed graphs, Southeast Asian Bull. Math., Vol. 36, 2012, No. 3, 389–397.
- Rao, S. B. Characterizations of harmonious marked graphs and consistent nets, J. Comb. Inf. & Syst. Sci., Vol. 9, 1984, No. 2, 97–112.
- Sampathkumar, E. Point-signed and line-signed graphs, Karnatak Univ. Graph Theory Res. Rep., No. 1, 1973 [also see Abstract No. 1 in Graph Theory Newsletter, Vol. 2, 1972, No. 2; National Academy Science Letters, Vol. 7, 1984, 91–93.
- Sampathkumar, E., P. S. K. Reddy, M. S. Subramanya. The line n-sigraph of a symmetric n-sigraph, Southeast Asian Bull. Math., Vol. 34, 2010, No. 5, 953–958.
- Sastry, D. V. S., B. S. P. Raju. Graph equations for line graphs, total graphs, middle graphs and quasi-total graphs, Discrete Math., Vol. 48, 1984, No. 1, 113–119.
- Sinha, D. New frontiers in the theory of signed graph, Ph.D. Thesis, University of Delhi (Faculty of Technology), 2005.
- Sinha, D., P. Garg, Canonical consistency of signed line structures, Graph Theory Notes N. Y., Vol. 59, 2010, 22–27.
- Sinha, D., P. Garg, Balance and consistency of total signed graphs, Indian J. Math., Vol. 53, 2011, No. 1, 71–81.
- Sinha, D., P. Garg, Characterization of total signed graph and semi-total signed graphs, Int. J. Contemp. Math. Sciences, Vol. 6, 2011, No. 5, 221–228.
- Sinha, D., P. Garg, On the regularity of some signed graph structures, AKCE Int. J. Graphs Comb., Vol. 8, 2011, No. 1, 63–74.
- Sinha, D., P. Garg, Some results on semi-total signed graphs, Discuss. Math. Graph Theory, Vol. 31, 2011, No. 4, 625–638.
- West, D. B. Introduction to Graph Theory, Prentice-Hall of India Pvt. Ltd., 1996.
- Zaslavsky, T. A mathematical bibliography of signed and gain graphs and allied areas, VIII Edition, Electron. J. Combin., #DS8(1998).
- Zaslavsky, T. Glossary of signed and gain graphs and allied areas, II Edition, Electron. J. Combin., #DS9(1998).
- Zaslavsky, T. The canonical vertex signature and the cosets of the complete binary cycle space, submitted.
Related papers
Cite this paper
Sinha, D., & Garg, P. (2013). A characterization of canonically consistent total signed graphs. Notes on Number Theory and Discrete Mathematics, 19(3), 70-77.


