József Sándor
Notes on Number Theory and Discrete Mathematics, ISSN 1310–5132
Volume 19, 2013, Number 1, Pages 50–54
Full paper (PDF, 130 Kb)
Details
Authors and affiliations
József Sándor ![]()
Babeș-Bolyai University, Department of Mathematics
Str. Kogălniceanu nr. 1, 400084 Cluj-Napoca, Romania
Abstract
We determine the best positive constants a and b such that
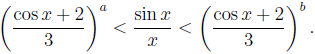
Similar sharp inequalities are also considered.
Keywords
- Inequalities
- Trigonometric functions
- Hyperbolic functions
- Monotonicity theorems
AMS Classification
- 26D05
- 26D07
- 26D99
References
- Hardy, G.H., J.E. Littlewood, G. Pólya. Inequalities, Cambridge Univ. Press, 1959.
- Neuman, E., J. Sándor, On some inequalities involving trigonometric and hyperbolic functions with emphasis on the Cusa–Huygens, Wilker, and Huygens inequalities, Math. Ineq. Appl., Vol. 13, 2010, No. 4, 715–723.
- Neuman, E., J. Sándor, Optimal inequalities for hyperbolic and trigonometric functions, Bull. Math. Anal. Appl., Vol. 3, 2011, No. 3, 177–181.
- Sándor, J., Two sharp inequalities for trigonometric and hyperbolic functions, ath. Ineq. Appl., to appear
Related papers
Cite this paper
Sándor, J. (2013). Sharp Cusa–Huygens and related inequalities. Notes on Number Theory and Discrete Mathematics, 19(1), 50-54.


