J. V. Leyendekkers and A. G. Shannon
Notes on Number Theory and Discrete Mathematics, ISSN 1310–5132
Volume 10, 2004, Number 1, Pages 1–11
Full paper (PDF, 159 Kb)
Details
Authors and affiliations
J. V. Leyendekkers
The University of Sydney, 2006 Australia
A. G. Shannon
Warrane College, Kensington, NSW 1465,
& KvB Institute of Technology, North Sydney, NSW 2060, Australia
Abstract
Modular-ring row structures are developed for squares. In particular, the row structures of even squares within the modular ring 
are analysed. This structure is shown to be linked via generalized pentagonal numbers to that of the odd squares. When 
, the link is via the triangular numbers. Equations could thus be developed for the rows of those primes that equal a sum of squares. Since the results are general they can be used to study in some depth those systems that have squares as a dominant feature.
AMS Classification
- 11A41
- 11A99
References
- J.V. Leyendekkers & A.G. Shannon, Powers as a Difference of Squares: The Effect on Triples. Notes on Number Theory & Discrete Mathematics. 8(3) 2002: 95-106.
- J.V. Leyendekkers, J.M. Rybak & A.G. Shannon, The Characteristics of Primes and Other Integers within the Modular Ring
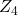and in Class 
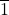. Notes on Number Theory & Discrete Mathematics. 4(1) 1998: 1-17. - J.V. Leyendekkers & A.G. Shannon, Some Characteristics of Primes within Modular Rings. Notes on Number Theory & Discrete Mathematics. In press.
- A.G. Shannon & A.F. Horadam, Generalized Fibonacci Number Triples,
American Mathematical Monthly, 80(2) 1973: 187-190.
Related papers
- Leyendekkers, J. V., & Shannon, A. G. (2002). Powers as a difference of squares: The effect on triples. Notes on Number Theory & Discrete Mathematics, 8(3), 95-106.
- Leyendekkers, J. V., Rybak, J. M., & Shannon, A. G. (1998). The characteristics of primes and other integers within the modular ring 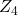and in class 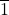. Notes on Number Theory & Discrete Mathematics, 4(1), 1-17.
- Leyendekkers, J. V., & Shannon, A. G. (2002). Some characteristics of primes within modular rings. Notes on Number Theory & Discrete Mathematics, 9(3), 49-58.
Cite this paper
Leyendekkers, J. V., & Shannon, A. G. (2004). The row structure of squares in modular rings. Notes on Number Theory and Discrete Mathematics, 10(1), 1-11.
