J. V. Leyendekkers and A. G. Shannon
Notes on Number Theory and Discrete Mathematics, ISSN 1310–5132
Volume 9, 2003, Number 3, Pages 49–58
Full paper (PDF, 3999 Kb)
Details
Authors and affiliations
J. V. Leyendekkers
The University of Sydney, 2006 Australia
A. G. Shannon
Warrane College, The University of New South Wales, 1465,
& KvB Institute of Technology, North Sydney, 2060, Australia
Abstract
The squares of primes in the Modular Ring ![]() fall in even rows,
fall in even rows, ![]() , in Class
, in Class ![]() with
with ![]() and
and ![]() (depending on the parity of
(depending on the parity of ![]() ). The
). The ![]() values are found to equal the rows that the primes occupy when
values are found to equal the rows that the primes occupy when ![]() is set as a tabular array. The primes in
is set as a tabular array. The primes in ![]() equal a unique sum or difference of squares
equal a unique sum or difference of squares ![]() and via
and via ![]() , the
, the ![]() pairs can be identified within the
pairs can be identified within the ![]() structure. The n values for composites follow well-defined linear functions that permit easy sorting. Finally, the parameter
structure. The n values for composites follow well-defined linear functions that permit easy sorting. Finally, the parameter ![]() in the well-known function
in the well-known function ![]() has been identified as the row in one or more of the Modular Rings
has been identified as the row in one or more of the Modular Rings ![]() or
or ![]() that contains one or more primes.
that contains one or more primes.
AMS Classification
- 11A07
- 11A41
References
- J. V. Leyendekkers, J.M. Rybak & A. G. Shannon. The Characteristics of Primes and Other Integers within the Modular Ring Z4 and in Class ̅14. Notes on Number Theory & Discrete Mathematics. 4(1) 1998: 1-17.
- J. V. Leyendekkers, J.M. Rybak & A. G. Shannon. The Characteristics of Primes and Other Integers within the Modular Ring Z4 and in class ̅3. Notes on Number Theory & Discrete Mathematics. 4(1) 1998: 18-37.
- J. V. Leyendekkers & A. G. Shannon. An Analysis of Mersenne-Fibonacci and Mersenne-Lucas Primes. Notes on Number Theory & Discrete Mathematics. 5(1) 1999: 1-26.
- J. V. Leyendekkers & A. G. Shannon. The Goldbach Conjecture Primes within a Modular Ring. Notes on Number Theory & Discrete Mathematics. 6(4) 2000: 101-112.
- J. V. Leyendekkers & A. G. Shannon. Twin Primes and the Modular Ring Z6. Notes on Number Theory & Discrete Mathematics. 7(4) 2001: 115-124.
- J. V. Leyendekkers & A. G. Shannon. An Analysis of Twin Primes h2n −1 Using Modular Rings Z6 and Z4. Notes on Number Theory & Discrete Mathematics. 7(1) 2001:21-28.
- J. V. Leyendekkers & A. G. Shannon. A Note on Twin Primes and the Modular Ring Z6. International Journal of Mathematical Education in Science & Technology. 33(2) 2002: 303-306.
- J. V. Leyendekkers & A. G. Shannon. Powers as a Difference of Squares: The Effect on Triples. Notes on Number Theory & Discrete Mathematics. 8(3) 2002: 95-106.
- J. V. Leyendekkers, J. M. Rybak & A. G. Shannon. Integer Class Properties Associates with an Integer Matrix. Notes on Number Theory & Discrete Mathematics. 1(2) 1995: 53-59.
- J. V. Leyendekkers, J. M. Rybak & A. G. Shannon. Analysis of Diophantine Properties Using Modular Rings with Four and Six Classes. Notes on Number Theory & Discrete Mathematics. 3(2) 1997: 61-74.
- Hans Riese Prime Numbers and Computer Methods for Factorization. Progress in Mathematics, Volume 126. Boston: Birkhauser, 1994.
- H. Beiler. Recreations in the Theory of Numbers. New York: Dover, 1964.
Related papers
- The analysis of twin primes within Z6
- The characteristics of primes and other integers within the modular ring Z4 and in class ̅3
- The characteristics of primes and other integers within the modular ring
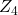 and in class
and in class 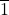
- The Goldberg-conjecture primes within a modular ring
- An analysis of Mersenne–Fibonacci and Mersenne–Lucas primes
- Analysis of Diophantine properties using modular rings with four and six classes
- Powers as a difference of squares: The effect on triples
- An analysis of twin primes h2n−1 using modular rings ℤ6 and ℤ4
- Integer class properties associated with an integer matrix
Cite this paper
Leyendekkers, J. V., & Shannon, A. G. (2003). Some characteristics of primes within modular rings. Notes on Number Theory and Discrete Mathematics, 9(3), 49-58.


