Zhiling Fan
Notes on Number Theory and Discrete Mathematics
Print ISSN 1310–5132, Online ISSN 2367–8275
Volume 31, 2025, Number 4, Pages 689–695
DOI: 10.7546/nntdm.2025.31.4.689-695
Full paper (PDF, 200 Kb)
Details
Authors and affiliations
Zhiling Fan ![]()
![]()
School of Mathematics and Statistics, Zhoukou Normal University
Zhoukou (Henan), China
Abstract
By making use of the Wallis’ integral formulae and integration by parts, two classes of infinite series are evaluated, in closed form, in terms of π and Riemann zeta function.
Keywords
- Infinite series
- Wallis formula
- Fourier series
- Riemann zeta function
2020 Mathematics Subject Classification
- 05A10
- 11B65
- 33C45
References
- Bhandari, N. (2022). Infinite series associated with the ratio and product of central binomial coefficients. Journal of Integer Sequences, 25, Article 22.6.5.
- Chu, W., & Zheng, D. (2009). Infinite series with harmonic numbers and central binomial coefficients. International Journal of Number Theory, 5(3), 429–448.
- Edwards, J. (1982). Differential Calculus (2nd edition). MacMilan, London.
- Gould, H. W. (1972). Combinatorial Identities: A Standardized Set of Tables Listing 500 Binomial Coefficient Summations. West Virginia, Morgantown Printing and Binding Co.
- Gradshteyn, I. S., & Ryzhik, I. M. (2007). Table of Series, Integrals, and Products (7th edition). Academic Press, Elsevier.
- Lehmer, D. H. (1985). Interesting series involving the central binomial coefficient. The American Mathematical Monthly, 92(7), 449–457.
- Zucker, I. J. (1985). On the series
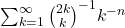 and related sums. Journal of Number Theory, 20(1), 92–102..
and related sums. Journal of Number Theory, 20(1), 92–102..
Manuscript history
- Received: 25 April 2025
- Revised: 10 September 2025
- Accepted: 17 September 2025
- Online First: 10 October 2025
Copyright information
![]() Ⓒ 2025 by the Authors.
Ⓒ 2025 by the Authors.
This is an Open Access paper distributed under the terms and conditions of the Creative Commons Attribution 4.0 International License (CC BY 4.0).
Related papers
Cite this paper
Fan, Z. (2025). Infinite series containing quotients of central binomial coefficients. Notes on Number Theory and Discrete Mathematics, 31(4), 689-695, DOI: 10.7546/nntdm.2025.31.4.689-695.


