Kanwara Mukkhata and Sompong Chuysurichay
Notes on Number Theory and Discrete Mathematics
Print ISSN 1310–5132, Online ISSN 2367–8275
Volume 31, 2025, Number 2, Pages 228–235
DOI: 10.7546/nntdm.2025.31.2.228-235
Full paper (PDF, 243 Kb)
Details
Authors and affiliations
Kanwara Mukkhata ![]()
Division of Computational Science, Faculty of Science, Prince of Songkla University
15 Kanchanavanit Rd, Hatyai, Songkhla 90110, Thailand
Sompong Chuysurichay ![]()
![]()
Division of Computational Science, Faculty of Science, Prince of Songkla University
15 Kanchanavanit Rd, Hatyai, Songkhla 90110, Thailand
Abstract
In this paper, we aim to provide alternative solutions of the Legendre’s equation ![]() where
where ![]() is a square-free positive integer. The results also lead to solutions of the well-known Pythagorean triples and Eisenstein triples.
is a square-free positive integer. The results also lead to solutions of the well-known Pythagorean triples and Eisenstein triples.
Keywords
- Diophantine equations
- Pythagorean triples
- Eisenstein triples
2020 Mathematics Subject Classification
- 11D09
- 11D72
References
- Abdelalim, S., & Dyani, H. (2014). The solution of the Diophantine equation
 . International Journal of Algebra, 8(15), 729–732.
. International Journal of Algebra, 8(15), 729–732. - Amato, R. (2017). A characterization of Pythagorean triples. JP Journal of Algebra, Number Theory and Applications, 39(2), 221–230.
- Andreescu, T., Andrica, D., & Cucurezeanu, I. (2010). An Introduction to Diophantine Equations: A Problem-Based Approach. Birkhauser, New York. ¨
- Cotronei, A. (2019). A characterization of Eisenstein triples. International Journal of Mathematics and Computer Science, 14(3), 583–590.
- Dubner, H., & Forbes, T. (2001). Prime Pythagorean triangles. Journal of Integer Sequences, 4(2), Article 01.2.3.
- Gordon, R. A. (2012). Properties of Eisenstein triples. Mathematics Magazine, 85(1), 12–25.
- Hudson, R. H., & Williams, K. S. (1983). On Legendre’s equation
 .Journal of Number Theory, 16(1), 100–105.
.Journal of Number Theory, 16(1), 100–105. - Mangalaeng, A. H. (2022). The primitive-solutions of Diohantine equation
 for primes
for primes 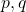 . Jurnal Matematika, Statistika dan Komputasi, 18(2), 308–314.
. Jurnal Matematika, Statistika dan Komputasi, 18(2), 308–314. - Tang, Q. (2021). On the Diophantine equation
 . Notes on Number Theory and Discrete Mathematics, 27(2), 88–100.
. Notes on Number Theory and Discrete Mathematics, 27(2), 88–100.
Manuscript history
- Received: 29 October 2024
- Revised: 4 May 2025
- Accepted: 5 May 2025
- Online First: 6 May 2025
Copyright information
![]() Ⓒ 2025 by the Authors.
Ⓒ 2025 by the Authors.
This is an Open Access paper distributed under the terms and conditions of the Creative Commons Attribution 4.0 International License (CC BY 4.0).
Related papers
- Tang, Q. (2021). On the Diophantine equation
 . Notes on Number Theory and Discrete Mathematics, 27(2), 88–100.
. Notes on Number Theory and Discrete Mathematics, 27(2), 88–100.
Cite this paper
Mukkhata, K. & Chuysurichay, S. (2025). Alternative solutions to the Legendre’s equation ![]() . Notes on Number Theory and Discrete Mathematics, 31(2), 228-235, DOI: 10.7546/nntdm.2025.31.2.228-235.
. Notes on Number Theory and Discrete Mathematics, 31(2), 228-235, DOI: 10.7546/nntdm.2025.31.2.228-235.


