József Sándor and Krassimir T. Atanassov
Notes on Number Theory and Discrete Mathematics
Print ISSN 1310–5132, Online ISSN 2367–8275
Volume 25, 2019, Number 4, Pages 8–15
DOI: 10.7546/nntdm.2019.25.4.8-15
Full paper (PDF, 198 Kb)
Details
Authors and affiliations
József Sándor ![]()
![]()
Department of Mathematics, Babes–Bolyai University
Str. Kogalniceanu 1, 400084 Cluj-Napoca, Romania
Krassimir T. Atanassov ![]()
Department of Bioinformatics and Mathematical Modelling
IBPhBME – Bulgarian Academy of Sciences,
Acad. G. Bonchev Str. Bl. 105, Sofia-1113, Bulgaria
Abstract
A new proof of solvability of equations
![]()
and
![]()
for ![]() are given. Connections with related problems and inequalities are pointed out, too.
are given. Connections with related problems and inequalities are pointed out, too.
Keywords
- Arithmetic function
- Balanced number
- Inequality
- Sum of divisors of a number
2010 Mathematics Subject Classification
- 11A25
- 26D15
References
- Sándor, J. (1990). An application of the Jensen–Hadamard inequality, Nieuw Arch. Wiskunde, 4 (8), 63–66.
- Sándor, J., Mitrinovic, D. S. & Crstici, B. (2006). Handbook of Number Theory, Vol. 1, Springer.
- Sándor, J. (2008). On equation
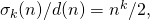 Octogon Math. Mag., 16 (1), 288–290.
Octogon Math. Mag., 16 (1), 288–290. - Sándor, J. & Kovacs, L. (2008). A note on the arithmetical functions
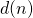 and
and 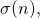 Octogon Math. Mag., 16 (1), 270–274.
Octogon Math. Mag., 16 (1), 270–274. - Sándor, J. (2009). A double-inequality for
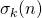 , Octogon Math. Mag., 17 (1), 285–287.
, Octogon Math. Mag., 17 (1), 285–287. - Sándor, J. (2009). A better lower bound for
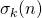 , Octogon Math. Mag., 17 (2), 767–768.
, Octogon Math. Mag., 17 (2), 767–768. - Sándor, J. & Kovacs, L. (2009). An inequality for the number of divisors of
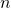 , Octogon Math. Mag., 17 (2), 746–750.
, Octogon Math. Mag., 17 (2), 746–750. - Sándor, J. (2014). An arithmetic inequality, An. St. Univ. Ovidius Constanta, 22 (1), 257–261.
- Subbarao, M. V. (1963). Balanced numbers, Solution of Problem E558, Amer. Math. Monthly, 70, 1009–1010.
- Vassilev-Missana, M., & Atanassov, K. (2007). A new point of view on perfect and other similar numbers, Advanced Studies on Contemporary Mathematics, 15 (2), 153–169.
Related papers
Cite this paper
Sándor, J. & Atanassov, K. (2019). A note on balanced numbers. Notes on Number Theory and Discrete Mathematics, 25(4), 8-15, DOI: 10.7546/nntdm.2019.25.4.8-15.


