A family of elliptic curves of rank ≥ 5 over ℚ(m)

Arman Shamsi Zargar and Naser Zamani
Notes on Number Theory and Discrete Mathematics
Print ISSN 1310–5132, Online ISSN 2367–8275
Volume 25, 2019, Number 4, Pages 24–29
DOI: 10.7546/nntdm.2019.25.4.24-29
Full paper (PDF, 172 Kb)

Details

Authors and affiliations

Arman Shamsi Zargar
Department of Mathematics and Applications, Faculty of Science
University of Mohaghegh Ardabili, Ardabil 56199-11367, Iran

Naser Zamani
Department of Mathematics and Applications, Faculty of Science
University of Mohaghegh Ardabili, Ardabil 56199-11367, Iran

Abstract

We construct a subfamily of elliptic curves E(r,s):(y-s)(y+s)=x(x-r)(x+r) with r=2(m^4-2m^3+2m^2+2m+1), s=2(m^2-2m-1)(m^2+1)^2, and show that its rank is at least five over \Bbb Q(m). This improves the previous results on the rank of the curves E(r,s) over \Bbb Q(m).

Keywords

  • Elliptic curves
  • Independence
  • Rank
  • Torsion subgroup

2010 Mathematics Subject Classification

  • 11G05
  • 14H52

References

  1. Antoniewicz, A. (2005). On a family of elliptic curves, Univ. Iagel. Acta Math., 43, 21–32.
  2. Birch, B. J., Stephens, N. M. (1996). The parity of the rank of the Mordell–Weil group,Topology, 5, 295–299.
  3. Brown, E. A., & Myers, B. T. (2002). Elliptic curves from Mordell to Diophantus and back,Amer. Math. Monthly, 109, 639–649
  4. Cremona, J. mwrank program, Available online at: http://homepages.warwick.ac.uk/staff/J.E.Cremona//ftp/progs/.
  5. Das, P., Juyal, A., & Moody, D. (2017). Integral isosceles triangle-parallelogram and Heron triangle-rhombus pairs with a common area and common perimeter, J. Number Theory, 180, 208–218.
  6. Duquesne, S., Nara, T., & Shamsi Zargar, A. (2019). Generators and integral points on elliptic curves associated with simplest quartic fields, Math. Slovaca, Accepted.
  7. Eikenberg, E. V. (2004). Rational Points on Some Families of Elliptic Curves, PhD thesis, University of Maryland.
  8. Fujita, Y.,& Nara, T. (2018). The Mordell–Weil base for the elliptic curve of the form 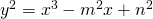y^2=x^3-m^2x+n^2, Publ. Math. Debrecen, 92, 1-2, 79–99.
  9. Izadi, F., & Baghalaghdam, M. (2018). Some new families of positive-rank elliptic curves arising from Pythagorean triples, Notes Number Theory Discrete Math., 24, 3, 27–36.
  10. Izadi, F., & Nabardi, K. (2016). A family of elliptic curves of rank 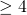\geq 4, Involve, 9, 5, 733–736.
  11. Izadi, F., & Shamsi Zargar, A. (2017). A note on twists of 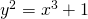y^2=x^3+1, Iran. J. Math. Sci. Inform., 12, 1, 27–34.
  12. Johnstone, J. A., & Spearman, B. K. (2010). Congruent number elliptic curves with rank at least three, Canad. Math. Bull., 53, 4, 661–666.
  13. Mestre, J.-F. (1986). Formules explicites et minorations de conducteurs de variétés algébriques, Compos. Math., 58, 209–232.
  14. Pari/gp, version 2.3.4, Available online at: http://pari.math.u-bordeaux.fr/
  15. Park, J., Poonen, B., Voight, J., & Wood, M. M. A heuristic for boundedness of ranks of elliptic curves, arXiv:1602.01431.
  16. Poonen, B. Heuristics for the arithmetic of elliptic curves, arXiv:1711.10112
  17. Sage software, Available online at: http://www.sagemath.org
  18. Silverman, J. H. (1983). Heights and the specialization map for families of abelian varieties, J. Reine Angew. Math., 342, 197–211.
  19. Tadić, P. (2012). On the family of elliptic curves 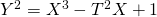Y^2=X^3-T^2X+1, Glas. Math. Ser. III, 47, 81–93.
  20. Tadić, P. (2012). The rank of certain subfamilies of elliptic curve 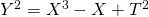Y^2=X^3-X+T^2, Ann. Math. Inform., 40, 145–153.
  21. Zhang, Y., Peng, J. Y., & Wang, J. M. (2018). Integral triangles and trapezoids pairs with a common area and a common perimeter, Forum Geom., 18, 371–380.
  22. Zhang, Y., & Shamsi Zargar, A. (2019). Integral triangles and cyclic quadrilateral pairs with a common area and a common perimeter, Forum Geom., Accepted.

Related papers

Cite this paper

Zargar, A. S. & Zamani, N. (2019). A family of elliptic curves of rank ≥ 5 over ℚ(m). Notes on Number Theory and Discrete Mathematics, 25(4), 24-29, DOI: 10.7546/nntdm.2019.25.4.24-29.

Comments are closed.