Numbers with the same kernel

Rafael Jakimczuk
Notes on Number Theory and Discrete Mathematics
Print ISSN 1310–5132, Online ISSN 2367–8275
Volume 25, 2019, Number 3, Pages 44–64
DOI: 10.7546/nntdm.2019.25.3.44-64
Full paper (PDF, 241 Kb)

Details

Authors and affiliations

Rafael Jakimczuk
Division Matematica, Universidad Nacional de Lujan
Buenos Aires, Argentina

Abstract

In this article we study functions related to numbers which have the same kernel. We apply the results obtained to the sums \sum_{n\leq x}\frac{1}{u(n)^s}, where s\geq 2 is an arbitrary but fixed positive integer and u(n) denotes the kernel of n. For example, we prove that

    \[\sum_{n\leq x}\frac{1}{u(n)^s}\sim f_{s}(x), \]

where

    \[f_{s}(x)=\sum^{\infty}_{k=1}\frac{b_{k,s}}{k!}(\log x)^k\]

and the positive coefficients b_{k,s} of the series have a strong connection with the prime numbers. We also prove that

    \[\sum_{n\leq x}\frac{1}{u(n)^s}=\exp\left(\left(\log x\right)^{\beta_s(x)}\right), \]

where \lim_{x\rightarrow \infty}\beta_s(x)=\frac{1}{s+1}. The methods used are very elementary. The case s=1, namely \sum_{n\leq x}\frac{1}{u(n)}, was studied, as it is well-known, by N. G. de Bruijn (1962) and W. Schwarz (1965).

Keywords

  • Kernel function
  • Numbers with the same kernel

2010 Mathematics Subject Classification

  • 11A99
  • 11B99

References

  1. Beukers, F. (1975). The lattice points of n-dimensional tetrahedra, Indag. Math., 37, 365–372.
  2. De Koninck, J., Diouf, I., & Doyon, N. (2012). On the truncated kernel function, J. Integer Seq., 15, Article 12.3.2.
  3. Hardy, G. H., & Wright, E. M. (1960). An Introduction to the Theory of Numbers, Oxford.
  4. Jakimczuk, R. (2008). An observation on the Cipolla’s expansion, Mathematical Sciences. Quarterly Journal, 2, 219–222.
  5. Jakimczuk, R. (2007). Integers of the form 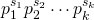p_1^{s_1}p_2^{s_2}\cdots p_k^{s_k}, where 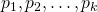p_1, p_2, \ldots, p_k are primes fixed, International Journal of Contemporary Mathematical Sciences, 2, 1327–1333.
  6. Jakimczuk, R. (2017). On the kernel function, International Mathematical Forum, 12, 693–703.
  7. Rey Pastor, J., Pi Calleja, P., & Trejo, C. A. (1969). Analisis Matematico, Volume 1, Kapelusz.

Related papers

Cite this paper

Jakimczuk, R. (2019). Numbers with the same kernel. Notes on Number Theory and Discrete Mathematics, 25(3), 44-64, DOI: 10.7546/nntdm.2019.25.3.44-64.

Comments are closed.