Volume 5, 1999, Number 4
Volume 5 ▶ Number 1 ▷ Number 2 ▷ Number 3 ▷ Number 4
Associated Legendre polynomials and Morgan-Voyce polynomials
Original research paper. Pages 125–134
A. F. Horadam
Full paper (PDF, 342 Kb)
One extremal problem. 9
Original research paper. Pages 135–137
K. Atanassov
Full paper (PDF, 81 Kb)
Number theoretic aspects of a combinatorial function
Original research paper. Pages 138–150
L. Halbeisen and N. Hungerbühler
Full paper (PDF, 434 Kb) | Abstract
We investigate number theoretic aspects of the integer sequence A000522 of Sloane’s On-Line Encyclopedia of Integer Sequences. This integer sequence counts the number of sequences without repetition one can build with n distinct objects. By introducing the notion of the “shadow” of an integer function – which is related to its divisors – we treat some number theoretic properties of this combinatorial function and investigate the related “irregular prime numbers”.
The Cardano family of equations
Original research paper. Pages 151–162
J. V. Leyendekkers and A. G. Shannon
Full paper (PDF, 391 Kb) | Abstract
The polynomial expansion of the Diophantine equation
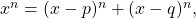
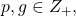
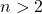
, yields roots of the form
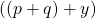
where
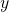
is a non-integer zero of a Cardano cubic polynomial of the form
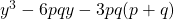
. This is a corollary to Fermat’s Last Theorem. The characteristics of this family are illustrated for
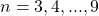
. For

odd,
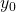
can be represented by
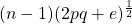
, and for

even there are two real values of
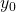
,
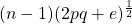
and
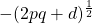
, where
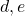
are real non-integer parameters. For a given

,

is simply related to
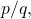
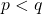
, and to a parameter
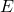
which is linear in

. The corresponding curves indicate the non-integral nature of
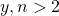
.
Volume 5 ▶ Number 1 ▷ Number 2 ▷ Number 3 ▷ Number 4


