A relation of modular discriminant Δ(τ)

Daeyeoul Kim
Notes on Number Theory and Discrete Mathematics, ISSN 1310-5132
Volume 3, 1997, Number 4, Pages 181—184
Download full paper: PDF, 156 Kb

Details

Authors and affiliations

Daeyeoul Kim
Department of Mathematics.
Chonbuk National University,
Chonju. 5G1-75G Korea

Abstract

Let \Delta(\Lambda_{tau}) = \Delta(\tau} be modular discriminant and \Omega(\tau) = (2\pi)^4\eta(\tau)^8, where \eta(\tau) be Dedekind \eta-function.

(a) \Delta(\tau) = \pm \frac{1}{16}\Omega(\frac{\tau + 1}{2})\Omega(\frac{\tau}{2})( \overline{\rho}\Omega(\frac{\tau + 1}{2}) + \rho\Omega((\frac{\tau}{2})).

(b) \Delta(\tau) = \pm \left ( \frac{1}{16}\Omega(\frac{\tau + 1}{2})^2\Omega(\frac{\tau}{2})^2 - 16\frac{h_1 (\tau)^2}{ \Omega (\frac{\tau}{2}) \Omega(\frac{\tau + 1}{2})} \right ).

References

  1. T. Apostol, Modular functions and Dirichlet series in Number theory. Springer -Verlag. New York, CJTM 41. 1976.
  2. K. Chandrasekharan. Elliptic Functions. Springer -Verlag. Grundlehren der mathematischen wis-sensrhaften 281. 1985.
  3. S. Chowla, Remarks on class-invariants and related topics. Seminar on Complex multiplication. Lecture Notes in Math 21 (1966), IV.1-10, Springer-Verlag, New York.
  4. E. Grosswald and H. Rachmacher. Dedekind sums, Cams Math. Monograph, Math. Assoc. of America. Providence. RI, 1972.
  5. K. Heon, Sphere packings and Jacobi theta series, master thesis of Chonbuk National Univ. (1997).
  6. P. Hwasin and K. Daeyeoul. A remark: of the Dedekind 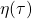\eta(\tau)-function and 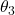\theta_3-series, E.1MS 5. no. 4 (1997), 611-622, Pushpa Publishing House, India.
  7. P. Hwasin and K. Daeyeoul, A study of the Dedekind 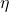\eta-function and modular discriminant, preprint.
  8. A. W. Knapp, Elliptic Curves, Mathematical Notes 40, Princeton University, Princeton, New .Jersey. 1992.
  9. S. Lang, Elliptic functions, Addison-Wesley, London, 1973.
  10. D. H. Lehmer. Ramanujan’s function r(n), Duke Math. J. 10 (1943), 483-492.
  11. A. OGG, Survey of modular functions of one variable, Modular Functions of One Variable I, Lecture Notes in Math 320 10 (1973), 1 35, Springer-Verlag, New York.
  12. G. Shimura. Introduction to the Arithmetic Theory of Automorphic Forms, Princeton Univ. Press, Princeton, N.J, 1971.
  13. C. L. Siegel, Topics m complex function theory, vol 1,2. Wiley-Interscience, 1969.
  14. H. Silverman. Advanced Topics in the. Arithmetic of Elliptic Curves, Springer Verlag. New York, 1994.
  15.  The Arithmetic of Elliptic Curves, Springer -Verlag, New York, 1986.
  16.  H. Stark. The Coates-Wilc.9 theorem revisited. In Number Theory related to Fermat’s Last. Theorem, N. Koblitz, ed. Birkhauser. Boston (1982). 349-362.
  17. T. Tate, The Arithmetic of Elliptic Curves, Invent. Math. 23 (1974), 171-206

Cite this paper

Kim, D. (1997). A relation of modular discriminant Δ(τ). Notes on Number Theory and Discrete Mathematics, 3(4), 181-184.

Comments are closed.