Yüksel Soykan, Nejla Özmen and Inci Okumuş
Notes on Number Theory and Discrete Mathematics
Print ISSN 1310–5132, Online ISSN 2367–8275
Volume 29, 2023, Number 3, Pages 571–588
DOI: 10.7546/nntdm.2023.29.3.571-588
Full paper (PDF, 240 Kb)
Details
Authors and affiliations
Yüksel Soykan ![]()
![]()
Department of Mathematics, Art and Science Faculty, Zonguldak Bülent Ecevit University
67100 Zonguldak, Turkey
Nejla Özmen ![]()
![]()
![]()
Department of Mathematics, Faculty of Art and Science, Duzce University
81620 Konuralp, Duzce, Turkey
Inci Okumuş ![]()
![]()
Department of Engineering Sciences, Faculty of Engineering, Istanbul University-Cerrahpasa
34320 Istanbul, Turkey
Abstract
In this paper, we examine generalized Tridovan sequences and treat in detail two cases called Tridovan sequences and Tridovan–Lucas sequences. We present Binet’s formulas, generating functions, Simson formulas, and the summation formulas for these sequences. In addition, we give some identities and matrices related to these sequences.
Keywords
- Tridovan numbers
- Tridovan–Lucas numbers
- Tetranacci numbers
2020 Mathematics Subject Classification
- 11B37
- 11B39
- 11B83
References
- Hathiwala, G. S., & Shah, D. V. (2017). Binet-Type Formula For The Sequence of Tetranacci Numbers by Alternate Methods. Mathematical Journal of Interdisciplinary Sciences, 6(1), 37–48.
- Horadam, A. F. (1965). Basic properties of a certain generalized sequence of numbers, The Fibonacci Quarterly, 3(3), 161–176.
- Howard, F. T., & Saidak, F. (2010). Zhou’s Theory of Constructing Identities. Congressus Numerantium, 200, 225–237.
- Brown, K. Perrin’s sequence. Mathpages. Available online at: https://www.
mathpages.com/home/kmath345/kmath345.htm - Melham, R. S. (1999). Some Analogs of the Identity
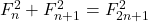 . The Fibonacci Quarterly, 39(4), 305–311.
. The Fibonacci Quarterly, 39(4), 305–311. - Natividad, L. R. (2013). On Solving Fibonacci-Like Sequences of Fourth, Fifth and Sixth Order. International Journal of Mathematics and Computing, 3(2), 38–40.
- Shannon, A. G., Anderson P. G., & Horadam, A. F. (2006). Properties of Cordonnier, Perrin and Van der Laan numbers. International Journal of Mathematical Education in Science and Technology, 37(7), 825–831.
- Singh, B., Bhadouria, P., Sikhwal, O., & Sisodiya, K. (2014). A Formula for Tetranacci-Like Sequence. General Mathematics Notes, 20(2), 136–141.
- Sloane, N. J. A. The On-line Encyclopedia of Integer Sequences. Available online at: http://oeis.org/.
- Soykan, Y. (2019). Simson Identity of Generalized m-step Fibonacci Numbers.
International Journal of Advances in Applied Mathematics and Mechanics, 7(2), 45–56. - Soykan, Y. (2019). Summation Formulas For Generalized Tetranacci Numbers. Asian Journal of Advanced Research and Reports, 7(2), 1–12.
- Soykan, Y. (2020). A study on generalized Tetranacci numbers: Closed form formulas
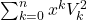 of Sums of the Squares of Term. Asian Research Journal of Mathematics, 16(10), 109–136.
of Sums of the Squares of Term. Asian Research Journal of Mathematics, 16(10), 109–136. - Soykan, Y. (2021). A study on the recurrence properties of generalized Tetranacci sequence. International Journal of Mathematics Trends and Technology, 67(8), 185–192.
- Soykan, Y. (2021). Properties of Generalized (r, s, t, u)-Numbers. Earthline Journal of Mathematical Sciences, 5(2), 297–327.
- Soykan, Y. (2023). On Generalized Padovan Numbers. International Journal of Advances in Applied Mathematics and Mechanics, 10(4), 72–90.
- Vieira, R. P. M., & Alves, F. R. V. (2019). Sequences of Tridovan and their identities. Notes on Number Theory and Discrete Mathematics, 25(3), 185–197.
- Waddill, M. E. (1967). Another generalized Fibonacci sequence. The Fibonacci Quarterly, 5(3), 209–227.
- Waddill, M. E. (1992). The Tetranacci sequence and generalizations. The Fibonacci Quarterly, 30(1), 9–20.
- Weisstein, E. W. Padovan Sequence. MathWorld–A Wolfram Web Resource. Available online at: https://mathworld.wolfram.com/PadovanSequence.html
- Weisstein, E. W. Perrin Sequence. MathWorld–A Wolfram Web Resource. Available online at: https://mathworld.wolfram.com/PerrinSequence.html
- Yilmaz, N., & Taskara, N. (2013). Matrix sequences in terms of Padovan and Perrin numbers. Journal of Applied Mathematics, 2013, Article ID 941673.
Manuscript history
- Received: 25 September 2022
- Revised: 28 July 2023
- Accepted: 14 August 2023
- Online First: 17 August 2023
Copyright information
![]() Ⓒ 2023 by the Authors.
Ⓒ 2023 by the Authors.
This is an Open Access paper distributed under the terms and conditions of the Creative Commons Attribution 4.0 International License (CC BY 4.0).
Related papers
Cite this paper
Soykan, Y., Özmen, N., Okumuş, I. (2023). On properties of generalized Tridovan numbers. Notes on Number Theory and Discrete Mathematics, 29(3), 571-588, DOI: 10.7546/nntdm.2023.29.3.571-588.


