A note on a broken Dirichlet convolution

Emil Daniel Schwab and Barnabás Bede
Notes on Number Theory and Discrete Mathematics, ISSN 1310–5132
Volume 20, 2014, Number 2, Pages 65–73
Full paper (PDF, 185 Kb)

Details

Authors and affiliations

Emil Daniel Schwab
Department of Mathematical Sciences, The University of Texas at El Paso
El Paso, TX 79968, USA

Barnabás Bede
Department of Mathematics, DigiPen Institute of Technology
Redmond, WA 98052, USA

Abstract

The paper deals with a broken Dirichlet convolution ⊗ which is based on using the odd divisors of integers. In addition to presenting characterizations of ⊗-multiplicative functions we also show an analogue of Menon’s identity:
\sum\limits_{\stackrel{a\ (mod\ n)}{(a,n)_{\otimes}=1}}{(a-1,n)}=\phi_{\otimes}(n)\left\tau(n)-\frac{1}{2}\tau_{2}(n)\right
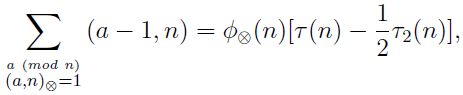
where (a, n)⊗ denotes the greatest common odd divisor of a and n, φ⊗(n) is the number of integers a (mod n) such that (a, n)⊗ = 1, τ(n) is the number of divisors of n, and τ2(n) is the number of even divisors of n.

Keywords

  • Dirichlet convolution
  • Möbius function
  • Multiplicative arithmetical functions
  • Menon’s identity

AMS Classification

  • 11A25

References

  1. Content, M., F. Lemay, P. Leroux, Catégories de Möbius et fonctorialités: Un cadre général pour l’inversion de Möbius, J. Combin. Theory Ser. A, Vol. 28, 1980, 169–190.
  2. Davison, T. M. K. On arithmetic convolutions, Canad. Math. Bull., Vol. 9, 1966, 287–296.
  3. Haukkanen, P. On the Davison convolution of arithmetical functions, Canad. Math. Bull., Vol. 32, 1989, 467–473.
  4. Haukkanen, P. On a formula for Euler’s totient function, Nieuw Arch. Wisk., Vol. 17, 1999, 343–348.
  5. Haukkanen, P. Menon’s identity with respect to a generalized divisibility relation, Aequationes Math., Vol. 70, 2005, 240–246.
  6. Kesava Menon, P. On the sum ∑(a − 1, n)[(a, n) = 1], J. Indian Math. Soc., Vol. 29, 1965, 155–163.
  7. Lawvere, F. W., M. Menni, The Hopf algebra of Möbius intervals, Theory and Appl. of Categories, Vol. 24, 2010, 221–265.
  8. Leinster, T. Notions of Möbius inversion, arXiv: 1201.0413 (2012).
  9. Leroux, P. Les catégories de Möbius, Cah. Topol. Géom. Diffé. Catég., Vol. 16, 1975, 280–282.
  10. McCarthy, P. J. Introduction to Arithmetical Functions Springer-Verlag, 1986.
  11. Schwab, E. D. Complete multiplicativity and complete additivity in Möbius categories,Italian J. Pure and Appl. Math., Vol. 3, 1998, 37–48.
  12. Schwab, E. D. Dirichlet convolution, bicyclic semigroup and a breaking process, Int. J. Number Th., Vol. 9, 2013, 1961–1972.

Related papers

Cite this paper

Schwab, E. D. & Bede, B. (2014). A note on a broken Dirichlet convolution. Notes on Number Theory and Discrete Mathematics, 20(2), 65-73.

Comments are closed.