S. Vidhyalakshmi, M. A. Gopalan, S. A. Thangam and Ö. Özer
Notes on Number Theory and Discrete Mathematics
Print ISSN 1310–5132, Online ISSN 2367–8275
Volume 25, 2019, Number 3, Pages 65-71
DOI: 10.7546/nntdm.2019.25.3.65-71
Full paper (PDF, 91 Kb)
Details
Authors and affiliations
S. Vidhyalakshmi ![]()
Department of Mathematics, Shrimati Indira Gandhi College
Trichy-620002, Tamil Nadu, India
M. A. Gopalan ![]()
Department of Mathematics, Shrimati Indira Gandhi College
Trichy-620002, Tamil Nadu, India
S. A. Thangam ![]()
Department of Mathematics, Shrimati Indira Gandhi College
Trichy-620002, Tamil Nadu, India
Ö. Özer ![]()
Department of Mathematics, Faculty of Science and Arts, Kırklareli University
Kırklareli, 39100, Turkey
Abstract
We obtain infinitely many non-zero integer triples (x, y, z) satisfying the non-homogeneous bi-quadratic equation with three unknowns 11(x2 – y2) + 3(x + y) =10z4. Various interesting properties among the values of x, y, z are presented. Some relations between the solutions and special numbers are exhibited.
Keywords
- Ternary bi-quadratic
- Integer solutions
- Pell equations
2010 Mathematics Subject Classification
- 11D25
- 11D09
References
- Carmichael, R. D. (1959). The Theory of Numbers and Diophantine Analysis, Dover Publications, New York.
- Dickson, L. E. (2005). History of Theory of Numbers, Diophantine Analysis. Volume 2, Dover Publications, New York.
- Gopalan, M. A., Vidhyalakshmi, S., & Devibala, S. (2010). Ternary bi-quadratic Diophantine equation
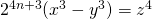 . Impact J. Sci. Tech, 4 (3), 57-60.
. Impact J. Sci. Tech, 4 (3), 57-60. - Gopalan, M. A., & Sangeetha, G. (2011). Integral solutions of ternary non-homogeneous bi-quadratic equation
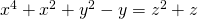 , Acta Ciencia Indica, XXXVIIM (4), 799-803.
, Acta Ciencia Indica, XXXVIIM (4), 799-803. - Gopalan, M. A., Vidhyalakshmi, S., & Sumathi, G. (2012). Integral solutions of ternary bi-quadratic non-homogeneous equation
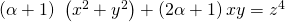 , JARCE, 6 (2), 97-98.
, JARCE, 6 (2), 97-98. - Gopalan, M. A., Sumathi, G., & Vidhyalakshmi, S. (2012). Integral solutions of ternary non-homogeneous bi-quadratic equation
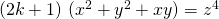 , Indian Journal of Engineering, 1 (1), 37-39.
, Indian Journal of Engineering, 1 (1), 37-39. - Gopalan, M.A. Vidhyalakshmi, S. Lakshmi, K. (2012). On the bi-quadratic equation with four unknowns
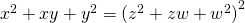 , IJPAMS, 5 (1), 73-77.
, IJPAMS, 5 (1), 73-77. - Gopalan, M. A., Sumathi, G., & Vidhyalakshmi, S. (2013). On the ternary bi-quadratic non-homogeneous equation
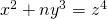 , Cayley J.Math, 2(2), 169-174.
, Cayley J.Math, 2(2), 169-174. - Gopalan, M. A., & Sivakami, B. (2013). Integral solutions of quartic equation with four unknowns
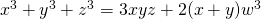 , Antartica J. Math., 10(2), 151-159.
, Antartica J. Math., 10(2), 151-159. - Gopalan, M. A., Vidhyalakshmi, S., & Kavitha, A. (2013). Integral solutions to the bi-quadratic equation with four unknowns
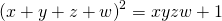 , IOSR, 7(4), 11-13.
, IOSR, 7(4), 11-13. - Gopalan, M. A., Sangeetha, S., & Somanath, M. (2015). Integer solutions of non-homogeneous biquadratic equation with four unknowns
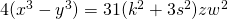 , Jamal Academic Research Journal, Special Issue, 296-299.
, Jamal Academic Research Journal, Special Issue, 296-299. - Gopalan, M. A., Vidhyalaksfmi, S., & Özer, Ö. (2018). A Collection of Pellian Equation (Solutions and Properties), Akinik Publications, New Delhi.
- Meena, K., Vidhyalakshmi, S., Gopalan, M. A., & Thangam, S. A. (2014). On the
bi-quadratic equation with four unknowns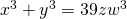 , International Journal of Engineering Research Online, 2(1), 57 -60.
, International Journal of Engineering Research Online, 2(1), 57 -60. - Mordell, L. J. (1969). Diophantine Equations, Academic press, New York.
- Telang, S. G. (1996). Number Theory, Tata Mc Graw Hill Publishing Company, New Delhi.
- Vijayasankar, A., Gopalan, M. A., & Kiruthika, V. (2018). On the bi-quadratic Diophantine equation with three unknowns
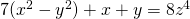 , International Journal of Advanced Scientific and Technical Research, 1 (8), 52-57.
, International Journal of Advanced Scientific and Technical Research, 1 (8), 52-57.
Related papers
Cite this paper
Vidhyalakshmi, S., Gopalan, M. A.,Thangam, S. A. & Özer, Ö. (2019). On ternary biquadratic Diophantine equation 11(x2 – y2) + 3(x + y ) =10z4 . Notes on Number Theory and Discrete Mathematics, 25(3), 65-71, DOI: 10.7546/nntdm.2019.25.3.65-71.


