The linear combination of two triangular numbers is a perfect square

Junyao Peng
Notes on Number Theory and Discrete Mathematics
Print ISSN 1310–5132, Online ISSN 2367–8275
Volume 25, 2019, Number 3, Pages 1–12
DOI: 10.7546/nntdm.2019.25.3.1-12
Full paper (PDF, 187 Kb)

Details

Authors and affiliations

Junyao Peng 
Chongqing Fuling No.15 Middle School
Chongqing, 400000, China

School of Mathematics and Statistics, Changsha University of Science and Technology
Hunan Provincial Key Laboratory of Mathematical Modeling and Analysis in Engineering
Changsha, 410114, China

Abstract

By the basic properties of Pell equation and the theory of congruence, we investigate the problem about the linear combination of two triangular numbers is a perfect square. First, we show that if 2n is not a perfect square, the Diophantine equation

    \[1+n\binom y 2=z^2\]

has infinitely many positive integer solutions (y,z). Second, we prove that if m,n are some special values, the Diophantine equation

    \[m\binom x 2+n\binom y 2=z^2\]

Keywords

  • Triangular number
  • Diophantine equation
  • Pell equation
  • Positive integer solution

2010 Mathematics Subject Classification

  • 11D09
  • 11D72

References

  1. Bencze, M. (2012). Proposed Problem 7508, Octogon Mathematical Magazine, 13(1B), 678.
  2. Chen, J. P. (2012). The squares with the form 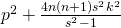p^2+\frac{4n(n+1)s^2k^2}{s^2-1}, Natural Science Journal of China West Normal University, 33(2), 196–198, 217.
  3. Cohen, H. (2007). Number theory, Vol. I: Tools and Diophantine Equations, Graduate Texts in Mathematics.
  4. Dickson, L. E. (1934). History of the Theory of Numbers, Vol. II: Diophantine Analysis, Dover Publications.
  5. Eggan, L. C., Eggan, P. C., & Selfridge, J. L. (1982). Polygonal products of polygonal numbers and the Pell equation, Fibonacci Quarterly, 20(1), 24–28.
  6. Guan, X. G. (2011). The squares with the form 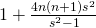1+\frac{4n(n+1)s^2}{s^2-1}, Natural Science Journal of Ningxia Teachers University, 32(3), 97–107.
  7. Hu, M. J. (2013). The positive integer solutions of the Diophantine equation 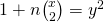1+n\binom x 2 =y^2, Journal of Zhejiang International Studies University, 4, 70–76.
  8. Ke, Z., & Sun, Q. (1980). Talk about the Indeterminate Equation, Harbin Institute of Technology Press.
  9. Le, M. H. (2007). The squares with the form 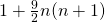1+\frac{9}{2}n(n+1), Natural Science Journal of Hainan University, 25(1), 13–14.
  10. Ran, Y. X., Yan, S. J., Ran, Y. P., &Yang, X. Y. (2008). The squares with the form 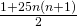\frac{1+25n(n+1)}{2}, Journal of Tianshui Normal University, 28(5), 9–15.
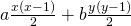  11. Sun, Z. H. (2009). On the number of representations of n by a\frac{x(x-1)}{2}+b\frac{y(y-1)}{2}, Journal of Number Theory, 129(5), 971–989.
  12. Wu, H. M. (2011). The square numbers with the form 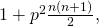1+p^2\frac{n(n+1)}{2}, Journal of Zhanjiang Normal College, 32(3), 20–22.

Related papers

Cite this paper

Peng, J. (2019). The linear combination of two triangular numbers is a perfect square. Notes on Number Theory and Discrete Mathematics, 25(3), 1-12, DOI: 10.7546/nntdm.2019.25.3.1-12.

Comments are closed.