Rafael Jakimczuk
Notes on Number Theory and Discrete Mathematics
Print ISSN 1310–5132, Online ISSN 2367–8275
Volume 22, 2016, Number 1, Pages 1–4
Full paper (PDF, 152 Kb)
Details
Authors and affiliations
Rafael Jakimczuk ![]()
División Matemática, Universidad Nacional de Luján
Buenos Aires, Argentina
Abstract
Let pn be the n-th prime number. The following limit is well-known
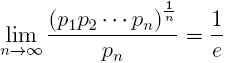
Let k be a fixed but arbitrary nonnegative integer. In this note we prove the more general limit
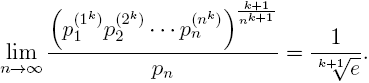
Keywords
- Prime numbers
- The e number
- Limits
AMS Classification
- 11A99
- 11B99
References
- Jakimczuk, R. (2007) The Ratio between the Average Factor in a Product and the Last Factor, Mathematical Sciences: Quarterly Journal, 1, 53–62.
- Jakimczuk, R. (2013) Sums of perfect powers, International Journal of Contemporary Mathematical Sciences, 8, 61–67.
- Jakimczuk, R. (2012) Asymptotic formulae for the n-th perfect power, Journal of Integer Sequences, 15, Article 12.5.5.
- Sándor J., & Verroken A. (2011) On a limit involving the product of prime numbers. Notes on Number Theory and Discrete Mathematics, 17(2), 1–3.
- Sándor J. (2012) On certain bounds and limits for prime numbers. Notes on Number Theory and Discrete Mathematics, 18(1), 1–5.
Related papers
Cite this paper
Jakimczuk, R. (2016). On a limit where appear prime numbers. Notes on Number Theory and Discrete Mathematics, 22(1), 1-4.


