Note on some explicit formulae for twin prime counting function

Mladen Vassilev-Missana
Notes on Number Theory and Discrete Mathematics, ISSN 1310–5132
Volume 19, 2013, Number 2, Pages 43–48
Full paper (PDF, 144 Kb)

Details

Authors and affiliations

Mladen Vassilev-Missana
5 V. Hugo Str., 1124 Sofia, Bulgaria

Abstract

In the paper for any integer n ≥ 5 the validity of the formula
\pi_2(n)= 1+\left\lfloor \sum_{k=1}^{\left\lfloor \frac{n+1}{6} \right\rfloor} \left(\frac{\vf(36\, k^2-1)}{36\, k^2-12k}\right)^{k^2} \right\rfloor
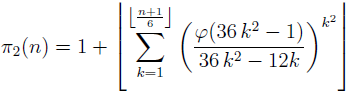
(where π2 denotes the twin prime counting function and φ is Euler’s totient function) is established. Also for any integer n ≥ 5 the formula
\pi_2(n)= 1+\left\lfloor \sum_{k=1}^{\left\lfloor \frac{n+1}{6} \right\rfloor} \left(\frac{\vf(36\, k^2-1)}{36\, k^2-12k}\right)^{6\,k \ln f(k)} \right\rfloor
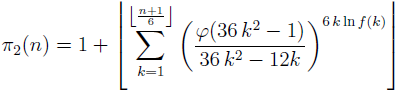
(where f is arbitrary artihmetic function with strictly positive values satisfying the condition
\sum\limits_{k=4}^{\infty}\frac{1}{f(k)}<1
is proved.

Keywords

  • Prime number (prime)
  • Twin primes
  • Twin prime counting function
  • Arithmetic function

AMS Classification

  • 11A25
  • 11A41

References

  1. Ribenboim, P. The New Book of Prime Number Records (3rd Edition), Springer-Verlag, New York, 1996.
  2. Vassilev-Missana, M. Some new formulae for the twin prime counting function π2. Notes on Number Theory and Discrete Mathematics, Vol 7, 2001, No. 1, 10–14.

Related papers

Cite this paper

Vassilev-Missana, M. (2013). Note on some explicit formulae for twin prime counting function. Notes on Number Theory and Discrete Mathematics, 19(2), 43-48.

Comments are closed.