The auxiliary equation associated with the plastic number

A. G. Shannon, A. F. Horadam and Peter G. Anderson
Notes on Number Theory and Discrete Mathematics, ISSN 1310–5132
Volume 12, 2006, Number 1, Pages 1–12
Full paper (PDF, 112 Kb)

Details

Authors and affiliations

A. G. Shannon
KvB Institute of Technology, North Sydney, 2060 &
Warrane College, University of New South Wales, Kensington,1465, Australia

A. F. Horadam
The University of New England, Armidale, 2351, Australia

Peter G. Anderson
Department of Computer Science, Rochester Institute of Technology, NY14623-5608

Abstract

This paper looks at some of the properties of the auxiliary equation associated with the plastic number which, in turn, is related to the sequences of numbers {Pn}, {Qn} and {Rn}, respectively, defined by
Pn = Pn − 2 + Pn − 3, n > 3, P1 = 1, P2 = 1, P3 = 1,
Qn = Qn − 2 + Qn − 3, n > 3, Q1 = 0, Q2 = 2, Q3 = 3,
Rn = Rn − 2 + Rn − 3, n > 3, R1 = 1, R2 = 0, R3 = 1.
The dominant root of the associated auxiliary equation is found by a contraction process related to Bernoulli’s iteration and the Jacobi–Perron Algorithm. The latter is one way of generalizing the ordinary continued fraction algorithm and an alternative way is explored which also relates to the auxiliary equations of the sequences. Various methods for reduction of the order of the cubic auxiliary equation are also considered.

AMS Classification

  • 11B37
  • 12D10
  • 65D15

References

  1. A. T. Benjamin, J. J. Quinn & J. A. Rouse. “Fibinomial Identities.” 10th International Conference on Fibonacci Numbers and Their Applications, Flagstaff, Arizona, 24-28 June, 2002.
  2. Leon Bernstein. The Jacobi-Perron Algorithm. Its Theory and Application. Lecture Notes in Mathematics, 207, Springer-Verlag, Berlin, 1971.
  3. Leon Bernstein. “Zeros of the Functions 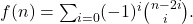f(n) = \sum_{i=0} (-1)^i \binom{n - 2i}{i}. Journal of Number Theory. 6 (1974): 264-270.
  4. L. Carlitz. “Generating Functions for Powers of Certain Sequences of Numbers.” Duke Mathematical Journal. 29 (1962): 521-537.
  5. H. R. P. Ferguson. “On a Generalization of the Fibonacci Numbers Useful in Memory Allocation Schema; or All about the Zeroes of k>0.” The Fibonacci Quarterly. 14 (1976): 223-243.
  6. W Galvin & R. Výborný. “Remarks on Rational Roots of a Cubic.” International Journal of Mathematical Education in Science & Technology. 34 (2003): 765-770.
  7. A. A. Gnanadoss. “Contracting Bernoulli’s Iteration and Recurrence Relations.” The Mathematical Gazette. 44 (1960): 221-223.
  8. M. Goldstern, R. F. Tichy & G. Turnwald. “Distribution of the Ratios of the Terms of a Linear Recurrence.” Monatshefte für Mathematik. 107 (1989): 35-55.
  9. P. Henrici. Discrete Variable Methods in Ordinary Differential Equations. New York: Wiley, 1962, Ch.5.
  10. F. B. Hildebrand. Introduction to Numerical Analysis. New York: McGraw-Hill, 1956, p.461.
  11. V. E. Hoggatt Jr & D. A. Lind. “Fibonacci and Binomial Properties of Weighted Compositions.” Journal of Combinatorial Theory. 4(1968): 121-124.
  12. A. F. Horadam. “Generating Functions for Powers of a Certain Generalized Sequence of Numbers.” Duke Mathematical Journal. 32 (1965): 437-446.
  13. A. F. Horadam. “Basic Properties of a Certain Generalized Sequence of Numbers.” The Fibonacci Quarterly. 3 (1965): 161-176.
  14. A. S. Householder. The Numerical Treatment of a Single Non-Linear Equation. New York: McGraw-Hill, 1970.
  15. E. C. Kennedy. “A Note on the Roots of a Cubic.” American Mathematical Monthly. 40 (1933): 411-412.
  16. G. A. Moore. “A Fibonacci Polynomial Sequence Defined by Multidimensional Continued Fractions; and Higher Order Golden Ratios.” The Fibonacci Quarterly. 31 (1993): 354-364.
  17. G. A. Moore. “The Limit of the Golden Numbers is 3/2.” The Fibonacci Quarterly. 32 (1994): 211-217.
  18. L. G. de Pillis. “Newton’s Cubic Roots.” Australian Mathematical Society Gazette. 25 (1998): 236-241.
  19. A. J. van der Poorten. “A Note on Recurrence Sequences.” Journal & Proceedings, Royal Society of New South Wales. 106 (1973): 115-117.
  20. H. Prodinger. “The Asymptotic Behaviour of the Golden Numbers.” The Fibonacci Quarterly. 34 (1996): 224-225.
  21. G. J. Rieger. “The Golden Section and Newton Approximation.” The Fibonacci Quarterly. 37 (1999): 178-179.
  22. A. G. Shannon. “The Jacobi-Perron Algorithm and Bernoulli’s Iteration.” The Mathematics Student. 42 (1974): 52-56.
  23. A. G. Shannon, Peter G. Anderson & A. F. Horadam, “Properties of Cordonnier, Perrin and van der Laan Numbers,” International Journal of Mathematical Education in Science and Technology, in press.
  24. A. G. Shannon & Leon Bernstein. “The Jacobi-Perron Algorithm and the Algebra of Recursive Sequences.” Bulletin of the Australian Mathematical Society. 8 (1972): 261-277.
  25. A. G. Shannon & A. F. Horadam. “Generating Functions for Powers of Third Order Recurrence Sequences.” Duke Mathematical Journal. 38 (1971): 791-794.
  26. A. Sofo. Summing Series using Residues. PhD Thesis, Victoria University of Technology, Melbourne, 1998.
  27. P. R. Turner. Numerical Analysis. London: Macmillan, 1994, pp.60-61.
  28. K.S. Williams. “A Generalization of Cardano’s Solution of the Cubic.” The Mathematical Gazette. 46 (1962): 221-223.

Related papers

  1. Atanassov, K., Dimitrov, D., & Shannon A. (2009). A remark on ψ-function and Pell-Padovan’s sequence. Notes on Number Theory and Discrete Mathematics, 15(2), 1-44.
  2. Deveci, Ö, & Shannon, A. G. (2017). Pell–Padovan-circulant sequences and their applications. Notes on Number Theory and Discrete Mathematics, 23(3), 100-114.
  3. Vieira, R. P. M. & Alves, F. R. V. (2019). Sequences of Tridovan and their identities. Notes on Number Theory and Discrete Mathematics, 25(3), 185-197.
  4. Shannon, A.G., Erdağ, Ö., & Deveci, Ö. (2021). On the connections between Pell numbers and Fibonacci p-numbers. Notes on Number Theory and Discrete Mathematics, 27(1), 148-160.
  5. İşbilir, Z., & Gürses, N. (2021). Pell–Padovan generalized quaternions. Notes on Number Theory and Discrete Mathematics, 27(1), 171-187.

Cite this paper

Shannon, A. G., Horadam, A. F., & Anderson, P. G. (2006). The auxiliary equation associated with the plastic number. Notes on Number Theory and Discrete Mathematics, 12(1), 1-12.

Comments are closed.