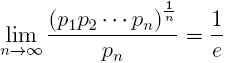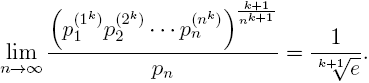Volume 22 ▶ Number 1 ▷ Number 2 ▷ Number 3 ▷ Number 4
Editorial
Editorial. Page i
Editors-in-Chief: Anthony Shannon, Krassimir Atanassov and József Sándor
Editorial (PDF, 25 Kb)
On a limit where appear prime numbers
Original research paper. Pages 1–4
Rafael Jakimczuk
Full paper (PDF, 153 Kb) | Abstract
Let
pn be the
n-th prime number. The following limit is well-known
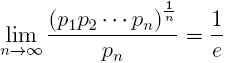
Let k be a fixed but arbitrary nonnegative integer. In this note we prove the more general limit
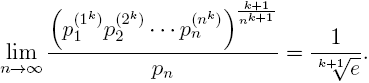
A note on Dedekind’s arithmetical function
Original research paper. Pages 5–7
József Sándor
Full paper (PDF, 140 Kb) | Abstract
We point out that an inequality published recently in [1] is a particular case of a general result from [4]. By another method, a refinement is offered, too. Related inequalities are also proved.
On an analogue of Buchstab’s identity
Original research paper. Pages 8–17
Debika Banerjee and Makoto Minamide
Full paper (PDF, 206 Kb) | Abstract
In this paper, let p denote a prime. We shall consider sums of the type Φ (x,y;f)= Σn≤p|n ⇒ p > y f(n) and ψ (x,y;f)=Σn≤p|n ⇒ p < y f(n) for certain kinds of arithmetical functions f and prove some identities for Φ and ψ which are analogous to the ‘so-called’ Buchstab identity. As an application, we will prove some formulas for square-free integers.
Inverse of triangular matrices and generalized bivariate Fibonacci and Lucas p-polynomials
Original research paper. Pages 18–28
Adem Şahin and Kenan Kaygısız
Full paper (PDF, 173 Kb) | Abstract
In this paper, we compute the generalized bivariate Fibonacci and Lucas p-polynomials by using inverse of various triangular matrices. In addition, in each calculation, instead of obtaining a type of sequence only, we are able to determine successive n terms of the two types of polynomial sequences simultaneously.
On the congruence ax − by ≡ c (mod p) and the finite field Zp
Original research paper. Pages 29–32
Anwar Ayyad
Full paper (PDF, 152 Kb) | Abstract
For prime p and 1 ≤ a, b, c < p let V be the algebraic set of the congruence ax − by ≡ c (mod p) in the plane. For an arbitrary box of size B we obtain a necessary and a sufficient conditions on the size B in order for the box to meet V. For arbitrary subsets S, T of Zp we also obtain a necessary and a sufficient conditions on the cardinalities of S, T so that S + T = Zp.
Some Golden Ratio generalized Fibonacci and Lucas sequences
Original research paper. Pages 33–41
J. V. Leyendekkers and A. G. Shannon
Full paper (PDF, 109 Kb) | Abstract
Various characteristics of the ordinary Fibonacci and Lucas sequences, many known for centuries, are shown to be common to generalized sequences related to the Golden Ratio. Periodicity properties are also investigated.
Set partitions and m-excedances
Original research paper. Pages 42–54
Toufik Mansour and Mark Shattuck
Full paper (PDF, 231 Kb) | Abstract
In this paper, we consider a generalized m-excedance statistic on set partitions which is analogous to the usual excedance statistic on permutations when m = 0. We study it from a probabilistic perspective in which set partitions are regarded as geometrically distributed words satisfying a so-called restricted growth property. We derive a general set of recurrences satisfied by the relevant generating functions and, in the m = 0 and m = 1 cases, find an explicit formula for the distribution of the statistic recording the number of m-excedances in partitions having a fixed number of blocks. When m = 0, one can also determine the joint distribution for the number of excedances with the major index statistic on set partitions. Further recurrences may be given in this case as well as formulas for the mean number of excedances and the variance.
Extended Pascal’s triangle
Original research paper. Pages 55–58
Krassimir T. Atanassov
Full paper (PDF, 127 Kb) | Abstract
An extension of the best known Pascal’s triangle is introduced and an explicit formula for its members is given.
On graphs whose Hosoya indices are primitive Pythagorean triples
Original research paper. Pages 59–80
Tomoe Kadoi and Yasuhide Numata
Full paper (PDF, 229 Kb) | Abstract
We discuss families of triples of graphs whose Hosoya indices are primitive Pythagorean triples. Hosoya gave a method to construct such families of caterpillars, i.e., trees whose vertices are within distance 1 of a central path. He also pointed out a common structure to the families. In this paper, we show the uniqueness of the common structure.
Volume 22 ▶ Number 1 ▷ Number 2 ▷ Number 3 ▷ Number 4