Volume 18 ▶ Number 1 ▷ Number 2 ▷ Number 3 ▷ Number 4
In Memoriam: Prof. Antal Bege (1962–2012)
Editorial. Pages 1–4
J. Sándor
Editorial (PDF, 107 Kb)
A modification of an elementary numerical inequality
Original research paper. Pages 5–7
Krassimir Atanassov
Full paper (PDF, 109 Kb) | Abstract
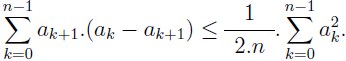
This is a modification of an inequality, previously introduced by the author.
Odd-powered triples and Pellian sequences
Original research paper. Pages 8–12
J. V. Leyendekkers and A. G. Shannon
Full paper (PDF, 123 Kb) | Abstract
Fibonacci numbers at most one away from a product of factorials
Original research paper. Pages 13–19
Diego Marques
Full paper (PDF, 166 Kb) | Abstract
Isomorphism testings for graph CG(a, b)
Original research paper. Pages 20–34
Worrawate Leela-Apiradee and Yotsanan Meemark
Full paper (PDF, 234 Kb) | Abstract
E = {{x, x + a}, {x, x + b}, {x, x − a}, {x, x − b} : x ∈ G}.
In this work, we use the properties of finite abelian group to derive isomorphism testing on the graph CG(a, b) defined above. We study classes of isomorphic graphs. This work generalizes Nicoloso and Pietropaoli’s paper
A new elementary proof of the inequality φ(n) > π (n)
Original research paper. Pages 35–37
Carlo Sanna
Full paper (PDF, 131 Kb) | Abstract
Generalized differential operators
Original research paper. Pages 38–44
A. G. Shannon
Full paper (PDF, 44 Kb) | Abstract
A note on sumsets and difference sets in ℤ/nℤ
Original research paper. Pages 45–47
Christopher J. Richardson and Craig V. Spencer
Full paper (PDF, 168 Kb) | Abstract
The Irrationals: A Story of the Numbers You Can’t Count On by Julian Havil
Book review. Page 48
Anthony Shannon
Book review (PDF, 107 Kb)


