Volume 18 ▶ Number 1 ▷ Number 2 ▷ Number 3 ▷ Number 4
A new proof of Lucas’ Theorem
Original research paper. Pages 1–6
Alexandre Laugier and Manjil P. Saikia
Full paper (PDF, 171 Kb) | Abstract
We give a new proof of Lucas’ Theorem in elementary number theory.
Pellian sequences and squares
Original research paper. Pages 7–10
J. V. Leyendekkers and A. G. Shannon
Full paper (PDF, 33 Kb) | Abstract
Elements of the Pell sequence satisfy a class of second order linear recurrence relations which interrelate a number of integer properties, such as elements of the rows of even and odd squares in the modular ring Z4. Integer Structure Analysis of this yields multiple-square equations exemplified by primitive Pythagorean triples, the Hoppenot equation and the equation for a sphere centred at the origin. The structure breaks down for higher powered triples so that solutions are blocked. However, Euler’s extension of Fermat’s Last Theorem does not work as the structure does permit multiple power equations such as a5 + b5 + c5 + d5 = e5.
On the polynomial and maximal solutions to a functional equation arising from multiplication of quantum integers
Original research paper. Pages 11–39
Lan Nguyen
Full paper (PDF, 257 Kb) | Abstract
We resolve two questions posed by Melvyn Nathanson, YangWang, and Alex Borisov concerning solutions with coefficients in ℚ of the functional equations arising from multiplication of quantum integers. First, we determine the necessary and sufficient criteria for determining when a rational function solution to these functional equations contains only polynomials. Second, we determine the sets of primes P for which there exist maximal solutions ΓP to these functional equations with support bases P. We also give an explicit description of these maximal solutions.
The common minimal equitable dominating signed graphs
Original research paper. Pages 40–46
P. Siva Kota Reddy and U. K. Misra
Full paper (PDF, 150 Kb) | Abstract
In this paper, we define the common minimal equitable dominating signed graph of a given signed graph and offer a structural characterization of common minimal equitable dominating signed graphs. In the sequel, we also obtained switching equivalence characterization:
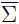
~
CMED(Σ), where
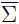
are
CMED(Σ) are complementary signed graph and common minimal equitable dominating signed graph of Σ respectively.
On Zagier’s conjecture for L(E, 2): A number field example
Original research paper. Pages 47–53
Jeffrey Stopple
Full paper (PDF, 164 Kb) | Abstract
We compute, for a CM elliptic curve E defined over a real quadratic field F, the details of an example of Zagier’s conjecture. This relates L(E, 2) to values of the elliptic dilogarithm function at a divisor in the Jacobian of E which arises from K-theory.
Solving algebraic equations with Integer Structure Analysis
Original research paper. Pages 54–60
J. V. Leyendekkers and A. G. Shannon
Full paper (PDF, 100 Kb) | Abstract
A new alternative method for solving algebraic equations is expounded. Integer Structure Analysis is used with an emphasis on parity, right-end-digits of the components and the modular ring Z5.
Generalized Hurwitz series
Original research paper. Pages 61–68
A. G. Shannon
Full paper (PDF, 99 Kb) | Abstract
Properties of generalized Hurwitz series are developed here in the framework of Fermatian numbers. These properties include derivatives in the Fontené–Jackson calculus which results in another solution of Ward’s Staudt–Clausen problem.
Remark on the hollow triangular and quadratic numbers
Original research paper. Pages 69–70
Krassimir Atanassov
Full paper (PDF, 133 Kb) | Abstract
A new concept related to the n-gonal numbers is introduced and it is illustrated with the cases of triangular and quadratic numbers.
A comment on a result of Virgolici
Original research paper. Pages 71–72
Mickey Polasub
Full paper (PDF, 103 Kb) | Abstract
We provide a short proof of a generalization of a recent result of Virgolici on the diophantine equation 2x + 1009y = pz.
Volume 18 ▶ Number 1 ▷ Number 2 ▷ Number 3 ▷ Number 4


