A Diophantine equation about polygonal numbers

Yangcheng Li
Notes on Number Theory and Discrete Mathematics
Print ISSN 1310–5132, Online ISSN 2367–8275
Volume 27, 2021, Number 3, Pages 113–118
DOI: 10.7546/nntdm.2021.27.3.113-118
Full paper (PDF, 199 Kb)

Details

Authors and affiliations

Yangcheng Li
School of Mathematics and Statistics, Changsha University of Science and Technology,
Changsha, 410114, People’s Republic of China

Abstract

It is well known that the number P_k(x)=\frac{x((k-2)(x-1)+2)}{2} is called the x-th k-gonal number, where x\geq1,k\geq3. Many Diophantine equations about polygonal numbers have been studied. By the theory of Pell equation, we show that if G(k-2)(A(p-2)a^2+2Cab+B(q-2)b^2) is a positive integer but not a perfect square, (2A(p-2)\alpha-(p-4)A + 2C\beta+2D)a + (2B(q-2)\beta-(q-4)B+2C\alpha+2E)b>0, 2G(k-2)\gamma-(k-4)G+2H>0 and the Diophantine equation

    \[AP_p(x)+BP_q(y)+Cxy+Dx+Ey+F=GP_k(z)+Hz\]

has a nonnegative integer solution (\alpha,\beta,\gamma), then it has infinitely many positive integer solutions of the form (at + \alpha,bt + \beta,z), where p, q, k \geq 3 and p,q,k,a,b,t,A,B,G\in\mathbb{Z^+}, C,D,E,F,H\in\mathbb{Z}.

Keywords

  • Polygonal number
  • Diophantine equation
  • Pell equation
  • Positive integer solution

2020 Mathematics Subject Classification

  • 11D09
  • 11D72

References

  1. Bencze, M. (2012). Proposed problem 7508. Octogon Mathematical Magazine, 13(1B), 678.
  2. Cohen, H. (2007). Number Theory, Vol. I: Tools and Diophantine Equations, Graduate Texts in Mathematics.
  3. Deza, E., & Deza, M. M. (2012). Figurate Numbers, World Scientific.
  4. Dickson, L. E. (1934). History of the Theory of Numbers, Vol. II: Diophantine Analysis, Dover Publications.
  5. Guan, X. G. (2011). The squares with the form 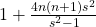1 + \frac{4n(n+1)s^2}{s^2 - 1} . Natural Science Journal of Ningxia Teachers University, 32(3), 97–107.
  6. Guy, R. K. (2007). Unsolved Problems in Number Theory. Springer-Verlag.
  7. Hamtat, A., & Behloul, D. (2017). On a Diophantine equation on triangular numbers. Miskolc Mathematical Notes, 18(2), 779–786.
  8. Hu, M. J. (2013). The positive integer solutions of the Diophantine equation 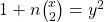1 + n \binom{x}{2} = y^2. Journal of Zhejiang International Studies University, 4, 70–76.
  9. Jiang, M., & Li, Y. C. (2020). The linear combination of two polygonal numbers is a perfect square. Notes on Number Theory and Discrete Mathematics, 26(2), 105–115.
  10. Le, M. H. (2007). The squares with the form 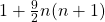1 + \frac{9}{2}n(n + 1). Natural Science Journal of Hainan University, 25(1), 13–14.
  11. Li, Y. C. (2020). Linear combinations of two polygonal numbers that take infinitely often a square value. Integers, 20, Article #A100.
  12. Peng, J. Y. (2019). The linear combination of two triangular numbers is a perfect square. Notes on Number Theory and Discrete Mathematics, 25(3), 1–12.
  13. Pla, J. (2014). On some subsets of the rational solutions of the equations 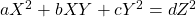aX^2+bXY +cY^2 = dZ^2. The Mathematical Gazette, 98(543), 424–428.
  14. Sastry, K. R. S. (1993). A triangular triangle problem. Crux Mathematicorum, 19(8), 219–221.
  15. Sastry, K. R. S. (1993). Pythagorean triangles of the polygonal numbers. Mathematics and Computer Education Journal, 27(2), 135–142.
  16. Scheffold, E. (2001). Pythagorean triples of polygonal numbers. The American Mathematical Monthly, 108(3), 257–258.

Related papers

Cite this paper

Li, Y. (2021). A Diophantine equation about polygonal numbers. Notes on Number Theory and Discrete Mathematics, 27(3), 113-118, DOI: 10.7546/nntdm.2021.27.3.113-118.

Comments are closed.