On the sum of three arbitrary Fibonacci and Lucas numbers

Nurettin Irmak, Zafer Şiar and Refik Keskin
Notes on Number Theory and Discrete Mathematics
Print ISSN 1310–5132, Online ISSN 2367–8275
Volume 25, 2019, Number 4, Pages 96–101
DOI: 10.7546/nntdm.2019.25.4.96-101
Full paper (PDF, 135 Kb)

Details

Authors and affiliations

Nurettin Irmak
Department of Mathematics, Ömer Halisdemir University Niğde, Turkey

Zafer Şiar
Department of Mathematics, Bingöl University Bingöl, Turkey

Refik Keskin
Department of Mathematics, Sakarya University Sakarya, Turkey

Abstract

In this paper, we solve the equations

   

   

   

   

for and a natural number . It is shown that only the equation has a finite number of solutions. The others have infinitely many solutions.

Keywords

• Fibonacci number
• Lucas number
• Rank
• Recurrences

2010 Mathematics Subject Classification

• 11B39
• 11D61
• 11B37

References

1. Bugeaud, Y., Mignotte, M. & Siksek, S. (2006). Classical and modular approaches to exponential Diophantine equations I. Fibonacci and Lucas perfect powers, Annals of Mathematics, 163 (3), 969–1018.
2. Carlitz, L. (1964). A note on Fibonacci numbers,The Fibonacci Quarterly, 2 (1), 15–28.
3. Farrokhi, D. G. M. (2007). Some remarks on the equation 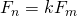in Fibonacci numbers,Journal of Integer Sequences, 10, Article 07.5.7.
4. Keskin, R. & Demirtürk Bitim, B. (2011). Fibonacci and Lucas congruences and their applications, Acta Mathematica Sinica (English Series), 27(4), 725–736.
5. Koshy, T. (2001). Fibonacci and Lucas Numbers with Applications, John Wiley and Sons, Proc., New York-Toronto.
6. Luca, F., & Szalay, L. (2009). Lucas Diophantine Triples,Integers, 9, 441–457.