On products of quartic polynomials over consecutive indices which are perfect squares

Kantaphon Kuhapatanakul, Natnicha Meeboomak and Kanyarat Thongsing
Notes on Number Theory and Discrete Mathematics
Print ISSN 1310–5132, Online ISSN 2367–8275
Volume 24, 2018, Number 3, Pages 56–61
DOI: 10.7546/nntdm.2018.24.3.56-61
Full paper (PDF, 146 Kb)

Details

Authors and affiliations

Kantaphon Kuhapatanakul
Department of Mathematics, Faculty of Science,
Kasetsart University, Bangkok, Thailand

Natnicha Meeboomak
Department of Mathematics, Faculty of Science,
Kasetsart University, Bangkok, Thailand

Kanyarat Thongsing
Department of Mathematics, Faculty of Science,
Kasetsart University, Bangkok, Thailand

Abstract

Let a be a positive integer. We study the Diophantine equation \prod_{k=1}^n (a^2 k^4 + (2a - a^2) k^2 +1) = y^2. This Diophantine equation generalizes a result of Gürel [5] for a=2. We also prove that the product (2^2 - 1)(3^2 - 1) \cdots (n^2 - 1) is a perfect square only for the values n for which the triangular number T^n is a perfect square.

Keywords

  • Diophantine equation
  • Perfect square
  • Quartic polynomial
  • Quadratic polynomial

2010 Mathematics Subject Classification

  • 11D25
  • 11D09

References

  1. Amdeberhan, T., Medina, L. A., & Moll, V. H. (2008) Arithmetical properties of a sequence arising from an arctangent sum, J. Number Theory, 128(6), 1807–1846.
  2. Chen, Y. G., Gong, M. L., & Ren, X. Z. (2013) On the products 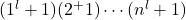(1^l + 1)(2^+1) \cdots (n^l +1), J. Number Theory, 133(8), 2470–2474.
  3. Cilleruelo, J. (2008) Squares in (1^2 + 1) \cdots (n^2+1), J. Number Theory, 128(8), 2488–2491.
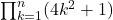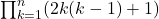  4. Fang, J. H. (2009) Neither \prod_{k=1}^n (4k^2 + 1) nor \prod_{k=1}^n (2k(k - 1) + 1) is a perfect square, Integers, 9, 177–180.
  5. Gürel, E. (2016) On the occurrence of perfect squares among values of certain polynomial products, Amer. Math. Monthly, 123(6), 597–599.
  6. Gürel, E. & Kisisel, A. U. O. (2010) A note on the products (1^{\mu} + 1) \cdots (n^{\mu} + 1). J. Number Theory, 130(1), 187–191.
  7. Sloane, N. J. A. (2011) The On-Line Encyclopedia of Integer Sequences. Published electronically at http://oeis.org.
  8. Yang, S., Togbé, A. & He, B. (2011) Diophantine equations with products of consecutive values of a quadratic polynomial, J. Number Theory, 131(5), 1840–1851.
  9. Zhang,W. &Wang, T. (2012) Powerful numbers in 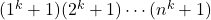(1^k + 1)(2^k + 1) \cdots (n^k + 1), J. Number Theory, 132(11), 2630–2635.

Related papers

  • Atanassov, K. T., Shannon, A. G., & Sándor, J. (2018). Editorial note. Notes on Number Theory and Discrete Mathematics, 24(4), 149-150.

Cite this paper

Kuhapatanakul, K., Meeboomak, N., & Thongsing, K. (2018). On products of quartic polynomials over consecutive indices which are perfect squares. Notes on Number Theory and Discrete Mathematics, 24(3), 56-61, DOI: 10.7546/nntdm.2018.24.3.56-61.

Comments are closed.