Mladen Vassilev-Missana
Notes on Number Theory and Discrete Mathematics, ISSN 1310–5132
Volume 19, 2013, Number 2, Pages 43–48
Full paper (PDF, 144 Kb)
Details
Authors and affiliations
Mladen Vassilev-Missana ![]()
5 V. Hugo Str., 1124 Sofia, Bulgaria
Abstract
In the paper for any integer n ≥ 5 the validity of the formula
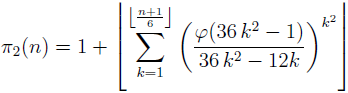
(where π2 denotes the twin prime counting function and φ is Euler’s totient function) is established. Also for any integer n ≥ 5 the formula
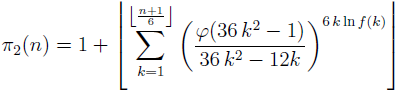
(where f is arbitrary artihmetic function with strictly positive values satisfying the condition
![]()
is proved.
Keywords
- Prime number (prime)
- Twin primes
- Twin prime counting function
- Arithmetic function
AMS Classification
- 11A25
- 11A41
References
- Ribenboim, P. The New Book of Prime Number Records (3rd Edition), Springer-Verlag, New York, 1996.
- Vassilev-Missana, M. Some new formulae for the twin prime counting function π2. Notes on Number Theory and Discrete Mathematics, Vol 7, 2001, No. 1, 10–14.
Related papers
Cite this paper
Vassilev-Missana, M. (2013). Note on some explicit formulae for twin prime counting function. Notes on Number Theory and Discrete Mathematics, 19(2), 43-48.


