Using integer structure to calculate the number of primes in a given interval

J. V. Leyendekkers and A. G. Shannon
Notes on Number Theory and Discrete Mathematics, ISSN 1310–5132
Volume 10, 2004, Number 3, Pages 77–83
Full paper (PDF, 111 Kb)

Details

Authors and affiliations

J. V. Leyendekkers
The University of Sydney, 2006 Australia

A. G. Shannon
Warrane College, Kensington, NSW 1465,
& KvB Institute of Technology, North Sydney, NSW 2060, Australia

Abstract

With the exception of 2 and 3, primes are only found in two classes of the modular ring Z6. The rows of the tabular display of this ring which con­tain composites in these two classes are given by R = R0+ pt, t = 0, 1, 2, 3, …, in which R0 is a function of p that is class specific. The number of composites, nc, in the two classes can be calculated from:

n_c \in \overline{2}_6 = {\Sum_p^{p_L}(((N-p^2)/2p)+a)/3} - (Q_1 + Q_2)

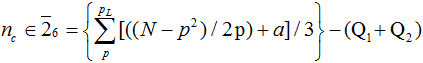
(a = 1 or 2 depending on the class of p),

n_C \in \overline{4}_6 = {\Sum_p^{p_L}(((N - p^2)/6p)+1) - (Q_3)}

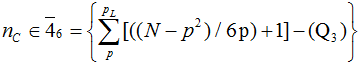
where pL is the prime less than and closest to √N. The Qi terms are quantities which arise from the characteristics of the factors of the composites. Subtraction of nc from the total integers in each class yields the number of primes for that class, and hence the total number of primes in the interval.

AMS Classification

  • 11A41
  • 11A07

References

  1. J.V. Leyendekkers & A.G. Shannon, The Analysis of Twin Primes within Z6. Notes on Number Theory & Discrete Mathematics. 7(4) 2001: 115-124.
  2. J.V. Leyendekkers & A.G. Shannon, Powers as a Difference of Squares: The Effect
    on Triples    . Notes on Number Theory & Discrete Mathematics. 8(3) 2002: 95-106.
  3. J.V. Leyendekkers & A.G. Shannon, Some Characteristics of Primes within Modular Rings. Notes on Number Theory & Discrete Mathematics. 9(3) 2003:49-58.
  4. J.V. Leyendekkers & A.G. Shannon, Analysis of Quadratic Diophantine Equations with Fibonacci-number Solutions. International Journal of Mathematical Education in Science & Technology. In press.
  5. J.V. Leyendekkers & A.G. Shannon, Structure of Fibonacci Numbers within Modular Rings. Notes on Number Theory & Discrete Mathematics. In press.
  6. Karl, Sabbagh, Dr Riemann’s Zeros. London: Atlantic Books, 2002.

Related papers

Cite this paper

Leyendekkers, J. V., and Shannon, A. G. (2004). Using integer structure to calculate the number of primes in a given interval. Notes on Number Theory and Discrete Mathematics, 10(3), 77-83.

Comments are closed.