Aldo Peretti
Notes on Number Theory and Discrete Mathematics, ISSN 1310–5132
Volume 3, 1997, Number 1, Pages 23–34
Full paper (PDF, 344 Kb)
Details
Authors and affiliations
Aldo Peretti
Facultad de Ciencia y Tecnologia – Universidad del Salvador
Rodriguez Peña 640
(1020) Buenos Aires, Argentina
Abstract
A new continued fraction is obtained for Euler constant ![]() , namely:
, namely:
![Rendered by QuickLaTeX.com \[C = \frac{1}{2} - \frac{1}{3} = \Bigg \{ \frac{ \Big ( \frac{2r - 1}{r-1} \Big )^2 \mid }{ \mid \frac{-2^r + r}{r(r+1)} } + \frac{2^r + r \mid}{ \mid r^2} + r^2 \Big \{ \frac{(2^r + m)^2 \mid }{ \mid 1} \Big \}_{m=1}^{m=2^r - 1} \Bigg \}_{r = 2}^{r = \infty} \]](https://nntdm.net/wp-content/ql-cache/quicklatex.com-a27a43d21d4e013a42e1d65c217236c1_l3.png)
It is considered the possibility to prove the irrationality and transcendency of the constant by means of this expansion.
References
- R. Ayoub: “Partial triumph or total failure?”. Math. Intelligencer, vol. 7, N° 2 (1985) p. 55-58.
- D. Bailey: “Numerical results on the transcendence of constants involving
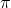 ,
,  and Euler’s constant”. Math. Comp. vol. 50, (1988) p. 275-282
and Euler’s constant”. Math. Comp. vol. 50, (1988) p. 275-282 - W. A. Beyer and M. S. Waterman: “Error analysis of a computation of Euler’s constant”. Math. Comp. vol. 28 (1974) p. 599-604
- W. A. Beyer and M. S. Waterman: “Decimals and partial quotients of Euler’s constant and Ln2”. Math. Comp. vol. 28 (1974) p. 667
- R. P. Brent: “Computation of the regular continued fraction for Euler’s constant”. Math. Comp. vol. 31 (1977) p. 771-777
- R. P. Brent and E. Me. Millan: “Some new algorithms for high precision computation of Euler’s constant”. Math. Comp. vol. 34 (1980) p. 305-312
- A. Froda: “La constante d’Euler est irrationelle”. Atti. Accad. Naz. Lincei, Rend. Cl. Sci. Fis. Mat. Natur. (8) 38 (1965) p. 338-344
- A. Froda: “Nouveaux criteres parametriques d’irrationalite”. C. R. Acad. Sci. Paris 261 (1965) p. 3012-3015
- J. W. Glaisher: “History of Euler’s constant”. Messenger of Math. Vol. 1 (1872) p. 25- 30
- H. W. Gould: “Some formulas for Euler’s constant”. Bull. Numb. Theory. Vol. X (1986) N° 2, p. 2-9
- Hermite-Stieltjes: Correspondance. Lettre 216, p.459, Gauthier Villars, Paris (1905).
- S. Selberg: “Bemerkung zu einer arbeit von Viggo Bran über die Riemannsche zetafunktion”. Norske Vid. Selsk. Forh. XIII N° 5 (1940), p. 17-19
- D. W. Sweeney: “On the computation of Euler’s constant”. Math. Comp. 17 (1963), p. 170-178
- O. Perron: “Die Lehre von Kettenbriichen”. 2nd. Edition, 1929. Teubner, Leipzig
- C. Brezinski: “History of Continued Fractions and Pade Approximants”. Springer Verlag. 1991
- G. Carr: “Formulas and theorems in Mathematics”. Chelsea edition.
Related papers
Cite this paper
Peretti, A. (1997). A new continued fraction for Euler’s constant. Notes on Number Theory and Discrete Mathematics, 3(1), 23-34.


