On the distribution of k-free numbers and r-tuples of k-free numbers. A survey

Radoslav Tsvetkov
Notes on Number Theory and Discrete Mathematics
Print ISSN 1310–5132, Online ISSN 2367–8275
Volume 25, 2019, Number 3, Pages 207-222
DOI: 10.7546/nntdm.2019.25.3.207-222
Download full paper: PDF, 226 Kb

Details

Authors and affiliations

Radoslav Tsvetkov
Faculty of Applied Mathematics and Informatics, Technical University of Sofia
8, St.Kliment Ohridski Blvd. 1756 Sofia, Bulgaria

Abstract

This paper presents a brief survey of the current state of research the distribution of k-free numbers and r-tuples of k-free numbers. We state the main problems in the field, sketch their history and the basic machinery used to study them.

Keywords

  • k-free numbers
  • Consecutive k-free numbers
  • Asymptotic formula

2010 Mathematics Subject Classification

  • 11L05
  • 11N25
  • 11N37

References

  1. Axer, A. (1911). Über einige Grenzwert sätze, S.-B. Math.-Natur. K1. Akad. Wiss. Wien 120 (2a), 1253–1298.
  2. Baker, R. C. & Pintz, J. (1985). The distribution of squarefree numbers, Acta Arith., 46, 73–79.
  3. Bhargava, M. (2014). The geometric sieve and the density of squarefree values of invariant polynomials, arXiv:1402.0031 [math.NT].
  4. Bhargava, M., Shankar, A., & Wang, X. (2016). Squarefree values of polynomial discriminants I, arXiv:1611.09806 [math.NT].
  5. Brandes, J. (2013). Twins of s-free numbers, arXiv:1307.2066v1 [math.NT].
  6. Browning, T. D. (2011). Power-free values of polynomials, Arch. Math., 96, 139–150.
  7. Cao, X., & Zhai, W. (1998). The distribution of square-free numbers of the form {[n^c]}, Journal de Théorie des Nombres de Bordeaux, 10, 287–299.
  8. Cao, X., & Zhai, W. (2000). Multiple exponential sums with monomials, Acta Arith., 92, 195–213.
  9. Cao, X., & Zhai, W. (2008). The distribution of square-free numbers of the form {[n^c]}, II, Acta Math. Sinica (Chin. Ser.), 51, 1187–1194.
  10. Carlitz, L. (1932). On a problem in additive arithmetic II, Quart. J. Math., 3, 273–290.
  11. Dietmann, R. & Marmon, O. (2014). The density of twins of k-free numbers, arXiv:1307.2481v2 [math.NT].
  12. Dimitrov, S. I. (2018). Consecutive square-free numbers of a special form, arXiv:1702.03983v3 [math.NT].
  13. Dimitrov, S. I. (2018). Consecutive square-free numbers of the form [n^c], [n^c]+1, JP Journal of Algebra, Number Theory and Applications, 40 (6), 945–956.
  14. Dimitrov, S. I. (2018). Consecutive cube-free numbers of the form [n^c], [n^c]+1, Appl. Math. in Eng. and Econ.–44th. Int. Conf., AIP Conf. Proc., 2048, 050004.
  15. Dimitrov, S. I. (2018). Consecutive square-free numbers of the form 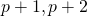p+1, p+2, Far East Journal of Mathematical Sciences, 107(2), 449–456.
  16. Dimitrov, S. I. (2019). On the number of pairs of positive integers 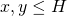x, y \leq H such that 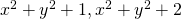x^2+y^2+1, x^2+y^2+2 are square-free, arXiv:1901.04838v1 [math.NT] 5 Jan 2019.
  17. Dudek, A. (2014). On the sum of a prime and a square-free number, arXiv:1410.7459v1 [math.NT].
  18. Erdős, P. (1953). Arithmetical properties of polynomials, J. London Math. Soc., 28, 416–425.
  19. Estermann, T. (1931). Einige sätze über quadratfeie zahlen, math. Ann., 105, 653–662.
  20. Filaseta, M. (1994). Powerfree values of binary forms, Journal of Number Theory, 49, 250–268.
  21. Greaves, G. (1992). Power-free values of binary forms, Q. J. Math, 43(1), 45–65.
  22. Güloğlu, A. M., & Nevans, C. W. (2008). Sums of multiplicative functions over a Beatty sequence, Bull. Austral. Math. Soc., 78, 327–334.
  23. Hablizel, M. (2016). The asymptotic behavior of limit-periodic functions on primes and an application to k-free numbers, arXiv:1609.08183v1 [math.NT] 26 Sep 2016.
  24. Heath-Brown, D. R. (1982). Prime numbers in short intervals and a generalized Vaughan identity, Canad. J. Math., 34, 1365–1377.
  25. Heath-Brown, D. R. (1984) The square-sieve and consecutive square-free numbers, Math. Ann., 266, 251–259.
  26. Heath-Brown, D. R. (2002). The density of rational points on curves and surfaces, Ann. of Math. 155 (2), 553–595.
  27. Heath-Brown, D. R. (2006). Counting rational points on algebraic varieties, Lecture Notes in Math., 1891, 51–95.
  28. Heath-Brown, D. R. (2009). Sums and differences of three k-th powers, J. Number Theory, 129, 1579–1594.
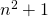  29. Heath-Brown, D. R. (2012), Square-free values of n^2+1, Acta Arith., 155, 1–13.
  30. Heath-Brown, D. R. (2013). Power-free values of polynomials, Quart. J. Math., 64, 177–188.
  31. Helfgott, H. (2007). Power-free values, large deviations and integer points on irrational curves, J. Theorie des Nombres de Bordeaux, 19, 433–472.
  32. Helfgott, H. (2008). Power-free values, repulsion between points, differing beliefs and the existence of error, CRM Proceedings and Lecture Notes, 46, 81–88.
  33. Helfgott, H. (2014). Square-free values of 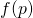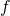f(p), f cubic, Acta Math., 213, 107–135.
  34. Hooley, C. (1967). On the power-free values of polynomials, Mathematika, 14, 21–26.
  35. Hooley, C. (1977). On the power-free numbers and polynomials II, J. Reine Angew. Math., 295, 1–21.
  36. Hooley, C. (2009). On the power-free values of polynomials in two variables, Analytic number theory, 235–266.
  37. Hooley, C. (2009). On the power-free values of polynomials in two variables: II, Journal of Number Theory, 129, 1443–1455.
  38. Jia, C. H. (1993). The distribution of squarefree numbers, Sci. China Ser. A, 36, 154–169.
  39. Lando, G. Square-free values of polynomials evaluated at primes over a function field, arXiv:1409.7633v3 [math.NT].
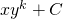  40. Lapkova, K. (2012). On the k-free values of the polynomial xy^k+C, Acta Math. Hung., 149, 190–207.
  41. Lapkova, K. & Xiao, S. (2018). Density of power-free values of polynomials, arXiv:1801.04481v1 [math.NT].
  42. Lee, J. & Murty, M. R. (2007). Dirichlet series and hyperelliptic curves, Forum Math., 19 (4), 677–705.
  43. Le Boudec, P. (2012). Power-free values of the polynomial 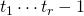t_1\cdots t_r-1, Bull. Aust. Math. Soc. , 85 (1), 154–163.
  44. Liu, H. & Zhang, W. (2005). On the squarefree and squarefull numbers, J. Math. Kyoto Univ., 45, 247–255.
  45. Liu, H. & Dong, H. (2015). On the distribution of consecutive square-free primitive roots modulo 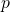p, Czechoslovak Mathematical Journal, 65, 555–564.
  46. Meng, Z. (2006). Some new results on k-free numbers, Journal of Number Theory, 121, 45–66.
  47. Mirsky, L. (1947). Note on an asymptotic formula connected with r-free integers, Quart. J. Math. Oxford, 18, 178–182.
  48. Mirsky, L. (1949). On the frequency of pairs of square-free numbers with a given difference, Bull. Amer. Math. Soc., 55, 936–939.
  49. Montgomery, H. L. & Vaughan, R. C. (1981). The distribution of squarefree numbers, Recent progress in analytic number theory, 1, (Durham, 1979), 247–256, Academic Press, London-New York.
  50. Nair, M. (1976). Power free values of polynomials, Mathematika, 23, 159–183.
  51. Nair, M. (1979). Power free values of polynomials II, Proc. London Math. Soc., 38, 353–368.
  52. Pasten, H. (2014). The ABC conjecture, arithmetic progressions of primes and square-free values of polynomials at prime arguments, Int. J. Number Theory DOI: 10.1142/S1793042115500396.
  53. Poonen, B. (2003). Squarefree values of multivariable polynomials, Duke Math. J., 118 (2), 353–373.
  54. Reuss, T. (2013). Power-free values of polynomials, arXiv:1307.2802v1 [math.NT].
  55. Reuss, T. (2014). Pairs of k-free numbers, consecutive square-full numbers, arXiv: 1212.3150v2 [math.NT].
  56. Ricci, G. (1933). Riecenche aritmetiche sui polynomials, Rend. Circ. Mat. Palermo, 57, 433–475.
  57. Rieger, G. J. (1978) Remark on a paper of Stux concerning square-free numbers in non-linear sequences, Pacific J. Math., 78, 241–242.
  58. Robert, O., & Sargos, P. (2006). Three-dimemsional exponential sums with monomials, J. Reine Angew. Math., 591, 1–20.
  59. Shapiro, H. N. (1983). Introduction to the Theory of Numbers, Pure and Applied Mathematics. Wiley-Interscience Publication, John Wiley & Sons, New York.
  60. Stewart, C., & Xiao, S. (2018). On the representations of k-free integers by binary forms, arXiv:1612.00487v2 [math.NT].
  61. Tolev, D. I. (2012) On the number of pairs of positive integers 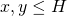x, y \leq H such that 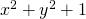x^2+y^2+1 is squarefree, Monatsh. Math., 165, 557–567.
  62. Tsang, K.-M. (1985). The distribution of r-tuples of square-free numbers, Mathematika, 32, 265–275.
  63. Uchiyama, S. (1972). On the power-free values of a polynomial, Tensor (N.S.), 24, 43–48.
  64. Victorovich, G. D. (2013). On additive property of arithmetic functions, Thesis, Moscow State University, (in Russian).
  65. Xiao, S. (2017). Power-free values of binary forms and the global determinant method, Int. Math. Res. Notices, 16, 5078–5135.
  66. Xiao, S. (2018). Square-free values of decomposable forms, Canadian Journal of Mathematics, 70, 1390–1415.
  67. Zhang, M. & Li, J. (2017). On the distribution of cube-free numbers with the form [n^ c], arXiv:1702.00165v1[math.NT].

Related papers

Cite this paper

Tsvetkov, R. (2019). On the distribution of k-free numbers and r-tuples of k-free numbers. A survey. Notes on Number Theory and Discrete Mathematics, 25(3), 207-222, doi: 10.7546/nntdm.2019.25.3.207-222.

Comments are closed.