Volume 14 ▶ Number 1 ▷ Number 2 ▷ Number 3 ▷ Number 4
Some combinatorial and recurrence relations for shapes in a trellis
Original research paper. Pages 1–10
J. Christos, R. Ollerton and A. Shannon
Full paper (PDF, 185 Kb) | Abstract
This paper considers the following problems from graph theory: in any section of given size of a trellis or wire-mesh fence, how many squares are there? how many rectangles are there? how many symmetric crosses are there? how many crosses in general? Certain patterns of arrays of numbers related to various substructures in terms of the numbers of edges and vertices in each case are listed and counted.
On an extremal problem related to the Delannoy numbers
Original research paper. Pages 11–14
Mladen Vassilev-Missana and Krassimir Atanassov
Full paper (PDF, 100 Kb) | Abstract
In the paper the maximal elements of the set {D(n − k, k | k = 0, 1, …, n} are found, where D(p, q) are the so-called Delannoy numbers and n ≥ 2 is a natural number. It is shown that for an even n the number D(n/2, n/2) is the maximal element of the mentioned set, while when n is odd – the maximal elements are two 
and 
.
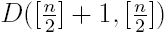
and .
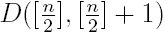
An interpretation of Pascual-Leone’s discrete mathematical model of human information processing capacity
Original research paper. Pages 15–20
A. G. Shannon
Full paper (PDF, 40 Kb) | Abstract
This paper outlines the pioneering work of Juan Pascal-Leone’s investigations of the cognitive load of learners. It utilized a recursive scheme in a Piagetian cognitive development framework to measure the maximum number of discrete “chunks” of information or schemes that our working memory can process, control or integrate at any one time. Pascal-Leone further designed a new compound-stimuli visual information type of task for testing his theories quantitatively. The stochastic model used for his predictions was the Bose–Einstein occupancy model of combinatorial analysis.
