Volume 6 ▶ Number 1 ▷ Number 2 ▷ Number 3 ▷ Number 4
Some remarks concerning the Bernoulli numbers
Original research paper. Pages 29–33
S. Tabirca
Full paper (PDF, 207 Kb) | Abstract
The aim of this article is to propose some remarks on the Bernoulli numbers. Firstly, a simple proof for the the equation
B2n+ 1 = 0 is presented. This proof also gives an equation for
ζ(2
k). Using a simple computation, the values of
ζ(2
k),
k = 1, 12 are presented. Finally, an equation for the infinite product
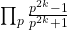
is proposed based on the Bernoulli numbers.
Some new equations concerning the Euler function
Original research paper. Pages 34–38
S. Tabirca and T. Tabirca
Full paper (PDF, 210 Kb) | Abstract
This article presents some new equations concerning the Euler function. An equation for the sum
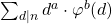
is found by using the multiplicative property. This is applied to find the sums
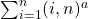
and
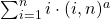
.
On prime k-tuples conjectures
Original research paper. Pages 39–44
V. Jotsov
Full paper (PDF, 193 Kb) | Abstract
There exist cases when experiments with the computational part of the research could lead to new theoretical proofs. New hypotheses are suggested in concern with the Hardy–Littlewood conjecture that there exist infinitely many prime k-tuples. Although all the details on the presented investigation are given in another scope papers (applied mathematical logic), the formulation of the presented hypotheses has an independent role. Strong relations are revealed with the investigations from Number Theory period before the Hardy and Littlewood down to the Greek system. The introduced formulas help to establish upper and lower bounds for different constellations of prime k-tuples.
On the one-sided orderability for semigroups
Original research paper. Pages 45–55
A. Baxhaku and M. Aslanski
Full paper (PDF, 358 Kb) | Abstract
In the papers of Merlier [5] and Saito [7] there are given some necessary and sufficient conditions on the linear orderability of the bands. Similar questions on semigroups are treated by Jordjev, Todorov [4] and Todorov [9]. In the last paper there are studied for the first time the one-sided orderable semigroups. We considerably enlarge the last studies, giving conditions under which a given semigroup should not be linearly orderable, (being perhaps left or right stable orderable) and conditions when a semigroup is not one sided orderable, or when it is no-one-sided orderable.
On the cardinal of the linear stable orders in a class of semigroups
Original research paper. Pages 56–60
A. Baxhaku and M. Aslanski
Full paper (PDF, 209 Kb) | Abstract
The main results are:
Theorem 1: For any semigroup
S generated by the non-idempotent elements
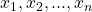
and the generating relations (i)
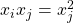
; (ii)
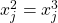
and (3)
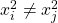
for
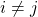
there exist
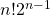
non dual two-sided stable orders and
![Rendered by QuickLaTeX.com \frac{1}{2}[(2n)! - n!2n]](https://nntdm.net/wp-content/ql-cache/quicklatex.com-e2fcb4181c7c700c171e222f33112425_l3.png)
(non dual) one sided stable orders which are not two sided stable ones and
Theorem 2: Let
S’ be a semigroup generated by the idempotents
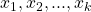
, the non-idempotents
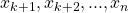
and the relations (i),(ii),(iii). Then the semigroup
S’ has
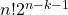
non-dual two-sided stable orders and
![Rendered by QuickLaTeX.com \frac{1}{2}[(2n - k)! -n!2^{n-k}]](https://nntdm.net/wp-content/ql-cache/quicklatex.com-273228146e3b706f521f6e9691280e96_l3.png)
only one-sided stable orders which are not two-sided stable ones.
Connections in mathematics: Fibonacci sequence via arithmetic progression
Original research paper. Pages 61–63
K. Atanassov
Full paper (PDF, 84 Kb)
On a formula related to the n-th partial sum of the harmonic series
Original research paper. Pages 64–68
M. Vassilev-Missana
Full paper (PDF, 139 Kb)
Volume 6 ▶ Number 1 ▷ Number 2 ▷ Number 3 ▷ Number 4


