Abdelmejid Bayad, Appolinaire Dossavi-Yovo, Alan Filipin, and Alain Togbé
Notes on Number Theory and Discrete Mathematics, ISSN 1310–5132
Volume 23, 2017, Number 3, Pages 1–26
Full paper (PDF, 246Kb
Details
Authors and affiliations
Abdelmejid Bayad ![]()
Departement de mathématiques, Université d’Evry Val d’Essonne ´
23 Bd. De France, 91037 Evry Cedex, France
Appolinaire Dossavi-Yovo ![]()
Institut de Mathematiques et de Sciences Physiques
Porto-Novo, Bénin
Alan Filipin ![]()
Faculty of Civil Engineering, University of Zagreb
Fra Andrije Kacica-Milosica 26, 10000 Zagreb, Croatia
Alain Togbé ![]()
Mathematics Department, Purdue University North Central
1401 S, U.S. 421, Westville IN 46391 USA
Abstract
In this paper, we prove that if ![]() , where
, where ![]() , is a
, is a ![]() -quadruple in the ring of Gaussian integers, then
-quadruple in the ring of Gaussian integers, then ![]() .
.
Keywords
- Diophantine m-tuple
- Pell equation
- Linear forms in logarithms
AMS Classification
- 11D09
- 11D45
- 11B37
- 11J86
References
- Baker, A. & Wüstholz, G. (1993) Logarithmic forms and group varieties, J. Reine Angew. Math. 442, 19–62.
- Bayad, A., Filipin, A. & Togbé, A. (2016) Extension of a parametric family of Diophantine triples in Gaussian integers, Acta Math. Hungar., 148(2), 312–327.
- Bennett, M. A. (1998) On the number of solutions of simultaneous Pell equations, J. Reine Angew. Math. 498 , 173–199.
- Cipu, M. & Trudgian, T. (2016) Searching for Diophantine quintuples, Acta Arith., 173, 365-382.
- Dujella, A. Diophantine
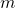 -tuples, http://web.math.pmf.unizg.hr/~duje/dtuples.html.
-tuples, http://web.math.pmf.unizg.hr/~duje/dtuples.html. - Dujella, A. (2001) An absolute bound for the size of Diophantine
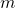 -tuples, J. Number Theory, 89, 126–150.
-tuples, J. Number Theory, 89, 126–150. - Dujella, A. (2004) There are only finitely many Diophantine quintuples, J. Reine Angew. Math. 566, 183–214.
- Franusic, Z. (2008) On the extensibility of Diophantine triples
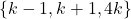 for Gaussian integers, Glas. Mat. Ser. III 43, 265–291.
for Gaussian integers, Glas. Mat. Ser. III 43, 265–291. - Fujita, Y. (2006) The unique representation
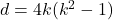 in
in 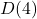 -quadruples
-quadruples 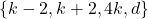 , Math. Commun. 11, 69–81.
, Math. Commun. 11, 69–81. - Jadrijevic, B. & Ziegler, V. (2006) A system of relative Pellian equations and related family of relative Thue equations, Int. J. Number Theory 2, 569–590.
Related papers
Cite this paper
Bayad, A., Dossavi-Yovo, A., Filipin, A., & Togbé, A. (2017). On the extensibility of the ![]() -triple
-triple ![]() over Gaussian integers. Notes on Number Theory and Discrete Mathematics, 23(3), 1-26.
over Gaussian integers. Notes on Number Theory and Discrete Mathematics, 23(3), 1-26.


