q-Volkenborn integration. II

T. Kim, L. C. Jang, D. W. Park and C. Adiga
Notes on Number Theory and Discrete Mathematics, ISSN 1310-5132
Volume 9, 2003, Number 4, Pages 83—89
Download full paper: PDF, 169 Kb

Details

Authors and affiliations

T. Kim
Institute of Science Education,
Kongju National University, Kongju 314-701, S. Korea

L. C. Jang
Department of Math. and Comput. Sci.,
KonKuk University, Chungju , Korea

D. W. Park
Department of Mathematics Education, Kongju
National University, Kongju 314-701, Korea

C. Adiga
Department of Studies in Math., Universuty
of Mysore, Mysore-570 006, India

Abstract

By using q-Volkenborn integration, the multiple Changhee q-Bernoulli numbers which are an interesting analogue of Barnes’ multiple Bernoulli numbers were constructed in [4]. The object of this paper is to define the extension of multiple Changhee q-Bernoulli numbers and to give the new explicit formulas which are related to these numbers.

Keywords

• p-adic q-integrals
• Multiple Barnes’ Bernoulli numbers

AMS Classification

• 11S80
• 11B68
• 11M99

References

1. E. W. Barnes, On the theory of the multiple gamma functions, Trans. Camb. Philos. Soc. 19 (1904), 374-425.
2. H.S.Cho, E.S.Kim, Translation-invariant p-adic integration on 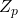Zp, Proc. Jangjeon Math. 3 (2001), 45-52.
3. T. Kim, Sums of products of q-Bernoulli numbers, Arch. Math. 76 (2001), 190-195.
4. T. Kim, Non-Arichimedean q-integrals associated with multiple Changhee q-Bernoulli polynomials, Russ. J. Math. Phys. 10(1) (2003), 91-98.
5. T. Kim, q-Volkenborn integration, Russ. J. Math. Phys. 9 (2002), 288-299.
6. T. Kim, q-Riemann zeta functions, to appear in Inter. J. Math. Math. Sci. (2004), 00-00.
7. T. Kim, An invariant p-adic integral associated with Daehee numbers, Integral Trans. Special Funct. 13 (2002), 65-69.
8. Y.H. Kim, D.W. Park, L.C.Jang, A note on q-analogue of Volkenborn integral, Adv. Stud. Contemp. Math. 4 (2002), 159-163.