A. Shannon and J. Clarke
Notes on Number Theory and Discrete Mathematics, ISSN 1310–5132
Volume 6, 2000, Number 1, Pages 14–22
Full paper (PDF, 276 Kb)
Details
Authors and affiliations
A. Shannon
KvB Institute of Technology, North Sydney, 2060, &
University of Technology, Sydney, 2007, Australia
J. Clarke
KvB Institute of Technology, North Sydney, 2060, &
University of Technology, Sydney, 2007, Australia
Abstract
This paper considers some properties associated with the dominant root of the characteristic polynomial of arbitrary order linear homogeneous recurrence relations with integer coefficients. In particular, it looks at computational issues for the general terms of the related sequences, and gives examples in terms of the Fibonacci numbers.
AMS Classification
- 11B39
- 11B37
- 11C08
References
- Bernstein, Leon. 1974. Zeros of the Function
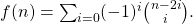 Journal of Number Theory. 6.4: 264-270.
Journal of Number Theory. 6.4: 264-270. - de Pillis, LG. 1998. Newton’s Cubic Roots. Australian Mathematical Society Gazette. 25.5: 236-241.
- Dickson, LE. 1952. History of the Theory of Numbers. Volume I. New York: Chelsea.
- Gilman, Leonard & Rose, AJ. 1984. APT: An Interactive Approach. Third Edition. New York: Wiley.
- Gnanadoss, AA. 1960. Contracting Bernoulli’s Iteration and Recurrence Relations. The Mathematical Gazette. 44: 221-223.
- Goldstem, M, Tichy, RF & Tumwald, G. Distribution of the Ratios of the Terms of a Linear Recurrence. Monatshefte fur Mathematik. 107.1: 35-55.
- Hoggatt, VE Jr & Lind, DA. 1968. Fibonacci and Binomial Properties of Weighted Compositions. Journal of Combinatorial Theory. 4.2: 121-124.
- Hoggatt, VE Jr & Bicknell-Johnson, M. 1979. Representation of Integers in Terms of Greatest Integer Functions and the Golden Section Ratio. The Fibonacci Quarterly. 17.4: 306.
- Horadam, AF. 1965. Basic Properties of a Certain Generalized Sequence of Numbers. The Fibonacci Quarterly. 3.3: 161-176.
- Mack, J.M. 1970a. A Note on Simultaneous Approximation. Bulletin of the Australian Mathematical Society. 3: 81-83.
- Mack, J.M. 1970b. The Continued Fraction Algorithm. Bulletin of the Australian Mathematical Society. 3: 413-422.
- Moore, GA. 1993. A Fibonacci Polynomial Sequence Defined by Multidimensional Continued Fractions; and Higher Order Golden Ratios. The Fibonacci Quarterly. 31.4: 354-364.
- Moore, GA. 1994. The Limit of the Golden Numbers is 3/2. The Fibonacci Quarterly. 32.3 211-217.
- Prodinger,H. 1996. The Asymptotic Behaviours of the Golden Numbers. The Fibonacci Quarterly. 34.3: 224-225.
- Rieger, GJ. 1999. The Golden Section and Newton Approximation. The Fibonacci Quarterly. 37.2: 178-179.
Related papers
Cite this paper
Clarke, J. & Shannon, A. (2000). Some aspects of the dominant root of a characteristic polynomial. Notes on Number Theory and Discrete Mathematics, 6(1), 14-22.


