The unitary analogue of Pillai’s arithmetical functions. II

László Tóth
Notes on Number Theory and Discrete Mathematics, ISSN 1310–5132
Volume 2, 1996, Number 2, Pages 40–46
Full paper (PDF, 277 Kb)

Details

Authors and affiliations

László Tóth
Department of Mathematics and Computer Science
“Babes-Bolyai” University
Str. M. Kogalniceanu 1
RO-3400 Cluj-Napoca, Romania

Abstract

Let k be a positive integer and let (a,b)_{*,k} denote the greatest k-th power divisor of a which is a unitary divisor of b. We introduce the function
\displaystyle P_k^*=\sum_{i=1}^{n^k}(i,n^k)_{*,k}

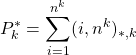
and obtain the arithmetical evaluation of it and an asymptotic formula for the summatory function of P_k^*, which improves for k = 1 an earlier result of the author.

References

  1. J. Chidambaraswamy and R. Sitaramachandrarao, Asymptotic results for a class of arithmetical functions, Mh. Math. 99(1985), 19-27.
  2. E. Cohen, Arithmetical functions associated with the unitary divisors of an integer, Math Z. 74(1960), 66-80.
  3. B. Gordon and E. Rogers, Sums of the divisor function, Canadian J. Math. 16(1964), 151-158.
  4. FI. G. Kopetzky, Bin asymptotischer Ausdruck fur eine zahlentheoretische Funktion, Mh. Math. 84(1977), 213-217.
  5. K. Nageswara Rao, On the unitary analogues of certain totients, Mh. Math. 70(1966), 149-154.
  6. S. S. Pillai, On an arithmetic function, J. Annamalai Univ. 2(1933), 243-248.
  7. M. V. Subbarao and D. Suryanarayana, Sums of the divisor and unitary divisor functions, J. Reine Angew. Math. 302(1978), 1-15.
  8. E. Teuffel, Aufgabe 599, Elem. Math. 25(1970), 65.
  9. L. Toth, The unitary analogue of Pillai’s arithmetical function, Collect. Math. 40(1989), 19-30.

Related papers

Cite this paper

Tóth, L. (1996). The unitary analogue of Pillai’s arithmetical functions. II. Notes on Number Theory and Discrete Mathematics, 2(2), 40-46.

Comments are closed.