On applications of blending generating functions of q-Apostol-type polynomials

Ugur Duran, Mehmet Acikgoz and Serkan Araci
Notes on Number Theory and Discrete Mathematics
Print ISSN 1310–5132, Online ISSN 2367–8275
Volume 25, 2019, Number 3, Pages 72-86
DOI: 10.7546/nntdm.2019.25.3.72-86
Full paper (PDF, 217 Kb)

Details

Authors and affiliations

Ugur Duran
Department of the Basic Concepts of Engineering
Faculty of Engineering and Natural Sciences
Iskenderun Technical University
TR-31200 Hatay, Turkey

Mehmet Acikgoz
Department of Mathematics
Faculty of Arts and Sciences
Gaziantep University
TR-27310 Gaziantep, Turkey

Serkan Araci
Department of Economics
Faculty of Economics, Administrative and Social Sciences
Hasan Kalyoncu University
TR-27410 Gaziantep, Turkey

Abstract

Motivated by Kurt’s blending generating functions of q-Apostol polynomials [16], we investigate some new identities and relations. We also aim to derive several new connections between these polynomials and generalized q-Stirling numbers of the second kind. Additionally, by making use of the fermionic p-adic integral over the p-adic numbers field, some relationships including unified Apostol-type q-polynomials and classical Euler numbers are obtained.

Keywords

• q-calculus
• Apostol–Bernoulli polynomials
• Apostol–Euler polynomials
• Apostol–Genocchi polynomials
• Stirling numbers of second kind
• Fermionic p-adic integral
• p-adic numbers

2010 Mathematics Subject Classification

• 05A30
• 11B68
• 11B73

References

1. Apostol, T. M. (1951). On the Lerch Zeta function, Pac. J. Math., 1 (2), 161–167.
2. Araci, S., & Acikgoz, M. (2012). A note on the Frobenius–Euler numbers and polynomials associated with Bernstein polynomials, Adv. Stud. Contemp. Math., 22 (3), 399–406.
3. Araci, S., Khan, W. A., Acikgoz, M., Özel, C., & Kumam, P. (2016). A new generalization of Apostol-type Hermite–Genocchi polynomials and its applications, SpringerPlus, 5, Article \# 860 (2016), doi. 10.1186/s40064-016-2357-4.
4. Bayad, A., & Kim, T. (2016). Identities for Apostol-type Frobenius–Euler polynomials resulting from the study of a nonlinear operator, Russ. J. Math. Phys., 23(2), 164–171.
5. Choi, J., Anderson, P.J., & Srivastava, H.M. (2008) Some -extensions of the Apostol–Bernoulli and the Apostol–Euler polynomials of order 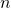, and the multiple Hurwitz zeta function, Appl. Math.Comput., 199, 723–737.
6. Duran, U., & Acikgoz, M. (2016). New identities for Carlitz’s twisted 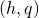-Euler polynomials under symmetric group of degree 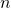, J. Ana. Num. Theor., 4 (I.2), 1–5.
7. El-Desouky, B. S., & Gomaa, R. S. (2014). A new unified family of generalized Apostol–Euler, Bernoulli and Genocchi polynomials, Appl. Math. Comput., 247, 695–702.
8. He, Y., Araci, S., Srivastava, H. M., & Acikgoz, M. (2015). Some new identities for the Apostol–Bernoulli polynomials and the Apostol–Genocchi polynomials, Appl. Math. Comput., 262, 31–41.
9. Kac, V., & Cheung, P. (2002). Quantum Calculus, Springer, New York.
10. Karande, B. K., & Thakare, N. K. (1975). On the unification of Bernoulli and Euler polynomials, Indian J. Pure Appl. Math., 6, 98–107.
11. Kim, D. S., Kim, T., Lee, S.-H., & Seo, J.-J. (2013). A note on -Frobenius–Euler numbers and polynomials, Adv. Stud. Theor. Phys., 7(18), 881–889.
12. Kim, T. (2009). Some identities on the -Euler polynomials of higher order and -Stirling numbers by the fermionic 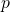-adic integral on 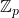, Russ. J. Math. Phys., DOI: 10.1134/S1061920809040037.
13. Kim, T. (2008). Symmetry 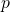-adic invariant integral on 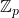for Bernoulli and Euler polynomials, J. Differ. Equ. Appl., 14, 1267–1277.
14. Kurt, B. (2016). A note on the Apostol-type -Frobenius–Euler polynomials and generalizations of the Srivastava–Pinter addition theorems, Filomat, 30 (1), 65–72.
15. Kurt, V. (2016). Some symmetry identities for the unified Apostol-type polynomials and multiple power sums, Filomat, 30 (3),583–592.
16. Kurt, B. (2016). Notes on unified -Apostol-type polynomials, Filomat, 30 (4), 921–927.
17. Kurt, V., & Kurt, B. (2016). Some identities and recurrence relations on the two variables Bernoulli, Euler and Genocchi polynomials, Filomat, 30 (7), 1757–1765.
18. Luo, Q.-M. (2004). On the Apostol–Bernoulli Polynomials, Cent. Eur. J. Math., 2 (4), 509–515.
19. Luo, Q.-M., & Srivastava, H. M. (2011). Some generalizations of the Apostol–Genocchi polynomials and the Stirling numbers of the second kind, Appl. Math. Comput., 217 (12), 5702–5728.
20. Luo, Q.-M., & Srivastava, H. M. (2006). Some relationships between the Apostol–Bernoulli and Apostol–Euler polynomials, Comput. Math. Appl., 51, 631–642.
21. Luo, Q.-M., & Srivastava, H. M. (2005). Some generalizations of the Apostol–Bernoulli and Apostol–Euler polynomials, J. Math. Anal. Appl., 308, 290–302.
22. Mahmudov, N. I. (2013). On a class of -Benoulli and -Euler polynomials, Adv. Difference Equ., 2013:108, doi:10.1186/1687-1847-2013-108.
23. Mahmudov, N. I., Keleshteri, M. E. (2014). -extension for the Apostol-type polynomials, J. Appl. Math., V.2014, ID 868167, 8 pages.
24. Mahmudov, N. I. (2012). -Analogues of the Bernoulli and Genocchi polynomials and the Srivastava-Pintér addition theorems, Discrete Dyn. Nat. Soc., Article ID 169348, 8 pages, DOI: 10.1155/2012/169348.
25. Mahmudov, N. I., & Keleshteri, M. E. (2013). On a class of generalized -Bernoulli and -Euler polynomials, Adv. Difference Equ., Article \# 115 (2013), DOI: 10.1186/1687-1847-2013-115.
26. Özarslan, M. A. (2011). Unified Apostol–Bernoulli, Euler and Genocchi polynomials, Comp. Math. Appl., 62, 2452–2462.
27. Özarslan, M. A. (2013). Hermite-based unified Apostol–Bernoulli, Euler and Genocchi polynomials, Adv. Difference Equ., 2013:116, 13 pages, doi:10.1186/1687-1847-2013-116.
28. Ozden, H. (2010). Unification of generating function of the Bernoulli, Euler and Genocchi numbers and polynomials, AIP Conf.Proc., 1281 (1), DOI: 10.1063/1.3497848.
29. Ozden, H., Simsek, Y., & Srivastava, H. M. (2010). A unified presentation of the generating function of the generalized Bernoulli, Euler and Genocchi polynomials, Comp. Math. Appl., 60 (10), 2779–2789.
30. Simsek, Y. (2012). Generating functions for -Apostol type Frobenius-Euler numbers and polynomials. Axioms, 1 (3), 395–403.
31. Srivastava, H. M. (2011). Some generalizations and basic (or -) extensions of the Bernoulli, Euler and Genocchi polynomials, Appl. Math. Inform. Sci., 5, 390–444.
32. Srivastava, H. M. (2000). Some formulas for the Bernoulli and Euler polynomials at rational arguments, Math. Proc. Cambridge Philos. Soc., 129, 77–84.
33. Srivastava, H. M., & Choi, J. (2012). Zeta and -Zeta functions and associated series and integrals, Elsevier Science Publishers, Amsterdam, The Netherlands.
34. Srivastava, H. M., Garg, M., & Choudhary, S. (2010). A new generalization of the Bernoulli and related polynomials, Russian J. Math. Phys., 17, 251–261.
35. Tremblay, R., Gaboury, S., &Fugère, B.-J. (2011). A new class of generalized Apostol–Bernoulli polynomials and some analogues of the Srivastava–Pintér addition theorem, Appl. Math. Lett., 24, 1888–1893.
36. Yasar, B. Y., & Özarslan, M. A. (2015). Frobenius–Euler and Frobenius–Genocchi polynomials and their differential equations, NTMSCI, 3 (2), 172–180.
37. Wang, W., Jia, C., & Wang, T. (2008). Some results on the Apostol–Bernoulli and Apostol–Euler polynomials, Comput. Math. Appl., 55, 1322–1332.