A combinatorial proof of multiple angle formulas involving Fibonacci and Lucas numbers

Fernando Córes and Diego Marques
Notes on Number Theory and Discrete Mathematics, ISSN 1310–5132
Volume 20, 2014, Number 5, Pages 35–39
Full paper (PDF, 137 Kb)

Details

Authors and affiliations

Fernando Córes
Department of Mathematics, University of Brasilia
Brasilia, DF, Brazi

Diego Marques
Department of Mathematics, University of Brasilia
Brasilia, DF, Brazi

Abstract

Let Fn and Ln be the n-th Fibonacci and Lucas number, respectively. In this note, we give a combinatorial proof for the following identity
F_{kn+p}=F_n^kF_p+\displaystyle\sum_{i=1}^kF_n^{i-1}(F_{n-1}F_{(k-i)n+p}+F_nF_{(k-i)n+p-1}).

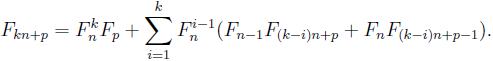
Keywords

  • Fibonacci
  • Lucas
  • Multiple angle
  • Combinatorial proof

AMS Classification

  • 11B39

References

  1. Koshy, T., Fibonacci and Lucas Numbers with Applications, Wiley, New York, 2001.
  2. Thongmoon, M., New identities for the even and odd Fibonacci and Lucas Numbers, Int. J. Contemp. Math. Sciences, Vol. 4, 2009, 671–676

Related papers

Cite this paper

Córes, F., & Marques, D. (2014). A combinatorial proof of multiple angle formulas involving Fibonacci and Lucas numbers. Notes on Number Theory and Discrete Mathematics, 20(5), 35-39.

Comments are closed.